
给出下列四个命题:
①命题“"xÎR,x2+1>0”的否定是“$x0ÎR,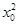 +1≤0”;
+1≤0”;
②曲线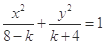 是椭圆的充要条件是
是椭圆的充要条件是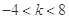 ;
;
③命题“若 ,则
,则 ”的逆命题是真命题;
”的逆命题是真命题;
④若"xÎR,4x2+4(a-2)x+1>0,则1<a<3.
其中正确的命题为 (只填正确命题的序号).
①④
【解析】
试题分析:因为全称命题的否定是存在性命题,更换连接词、否定结论,所以①命题“"xÎR,x2+1>0”的否定是“$x0ÎR,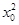 +1≤0”;是真命题;
+1≤0”;是真命题;
由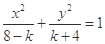 表示椭圆,可知
表示椭圆,可知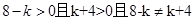 ,即
,即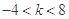 且
且 ,所以②曲线
,所以②曲线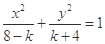 是椭圆的充要条件是
是椭圆的充要条件是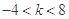 ;不正确;
;不正确;
命题“若 ,则
,则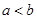 ”的逆命题是:命题“若
”的逆命题是:命题“若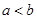 ,则
,则 ”,因为
”,因为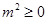 ,所以,③命题“若
,所以,③命题“若 ,则
,则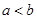 ”的逆命题是真命题;不正确;
”的逆命题是真命题;不正确;
④若"xÎR,4x2+4(a-2)x+1>0,则1<a<3.正确。因为"xÎR,4x2+4(a-2)x+1>0,
所以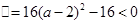 ,解得1<a<3。综上知正确的命题为①④。
,解得1<a<3。综上知正确的命题为①④。
考点:本题主要考查命题的概念,充要条件的概念,椭圆的标准方程。
点评:中档题,本题通过判断几个命题的真假,综合考查了全称命题、特称命题、椭圆的标准方程、不等式性质等,对考查学生灵活运用数学知识解题的能力有较好的考查。


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com