
(1)C到平面ABˊD的距离;
(2)A到平面CBˊD的距离;
(3)AC和平面CBˊD所成的角.
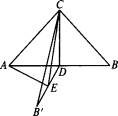
| 解:(1)∵CD⊥AD,CD⊥BˊD,
∴CD⊥平面ABˊD, ∴CD的长就是C到平面ABˊD的距离. 由△ABC是等腰直角三角形,AB=2,得CD=1, 即C到平面ABˊD的距离为1. (2)过点A作AE⊥BˊD交BˊD于E, ∵CD⊥平面ABˊD, ∴平面ABˊD⊥平面BˊCD, ∴AE⊥平面CBˊD. ∴AE的长为A到平面BˊCD的距离. ∵AD⊥CD,BˊD⊥CD, ∴∠ADBˊ为二面角A—CD—Bˊ的平面角. 由题意知∠ADBˊ=60°. 在Rt△ADE中,AD=1,∴AE= 即点A到平面CBˊD的距离为 (3)连结CE. ∵AE⊥平面BˊCD, ∴AC在平面BˊDC内的射影为CE, ∴∠ACE为AC和平面CBˊD所成的角. 在Rt△ACE中,AC= ∴sinACE= ∴∠ACE=arcsin 即AC与平面CBˊD所成的角为arcsin 点评:(2)中选作AE⊥BˊD于E,然后证AE是垂线段.最后再计算AE.(3)中选作∠ACE,然后证∠ACE是AC与平面BˊCD所成的角,最后再求出∠ACE,这一例题再一次说明了“作、证、算”是解决这类题目的基本步骤.
|


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
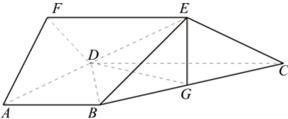 设多面体ABCDEF,已知AB∥CD∥EF,平面ABCD⊥平面ADF,其中ADF是以AD为斜边的等腰直角三角形,设G为BC的中点,若∠ADC=120°,AD=AB=2,CD=4,EF=3.
设多面体ABCDEF,已知AB∥CD∥EF,平面ABCD⊥平面ADF,其中ADF是以AD为斜边的等腰直角三角形,设G为BC的中点,若∠ADC=120°,AD=AB=2,CD=4,EF=3.查看答案和解析>>
科目:高中数学 来源: 题型:044
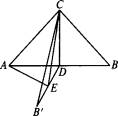
以等腰直角三角形ABC的斜边AB上的高CD为轴折成一个60°的二面角,使B到Bˊ的位置,已知斜边AB=2,求:
(1)C到平面ABˊD的距离;
(2)A到平面CBˊD的距离;
(3)AC和平面CBˊD所成的角.
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省开原市高二第三次月考理科数学 题型:选择题
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,将ΔABD和ΔACD折起,使折起后的ΔABC成等边三角形,则二面角C-AB-D的余弦值等于 ( )
A.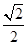 B.
B. C.
C.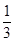 D.
D.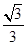
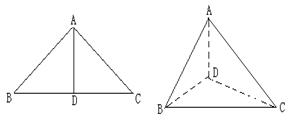
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年山西大学附中五模理) 以等腰直角三角形ABC的斜边BC上的高AD为折痕,将△ABC折起(如图),使折起后的△ABC恰成等边三角形,M为高AD的中点,则直线AB与CM所成角的余弦值为 .
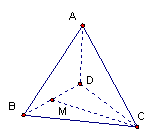
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com