
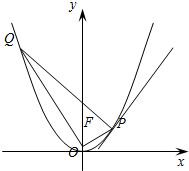
 已知抛物线C的顶点在原点, 焦点为F(0, 1).
已知抛物线C的顶点在原点, 焦点为F(0, 1).
(Ⅰ) 求抛物线C的方程;
(Ⅱ) 在抛物线C上是否存在点P, 使得过点P的直
线交C于另一点Q, 满足PF⊥QF, 且PQ与C
在点P处的切线垂直? 若存在, 求出点P的坐标;
若不存在, 请说明理由.
本题主要考查抛物线的几何性质,直线与抛物线的位置关系等基础知识,考查解析
几何的基本思想方法和综合解题能力。满分15分。
(Ⅰ) 解: 设抛物线C的方程是x2 = ay,
则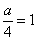 ,
,
即a = 4.
故所求抛物线C的方程为x2 = 4y . …………………(5分)
(Ⅱ) 解: 设P(x1, y1), Q(x2, y2),
则抛物线C在点P处的切线方程是
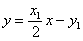 ,
,
直线PQ的方程是
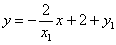 .
.
将上式代入抛物线C的方程, 得
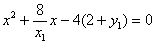 ,
,
故 x1+x2
=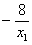 , x1x2 =-y1 ,
, x1x2 =-y1 ,
所以 x2=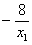 -x1 , y2=
-x1 , y2=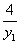 +y1+4
.
+y1+4
.
而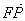 =(x1, y),
=(x1, y), 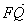 =(x2 , y) ,
=(x2 , y) ,
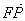 ×
×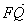 =x1 x2+(y) (y)
=x1 x2+(y) (y)
=x1 x2+y1 y2-(y1+y2)+1
=-4(2+y1)+
y1(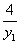 +y1+4)-(
+y1+4)-(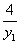 +2y1+4)+1
+2y1+4)+1
=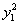 -2y1 -
-2y1 -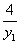 -7
-7
=(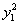 +2y1+1)-4(
+2y1+1)-4(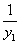 +y1+2)
+y1+2)
=(y1+1)2-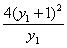
=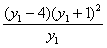
=0,
故 y1=4, 此时, 点P的坐标是(±4,4) .
经检验, 符合题意.
所以, 满足条件的点P存在, 其坐标为P(±4,4). …………………(15分)


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| |AB| | |FM| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com