
【题目】A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16;
B组:12,13,15,16,17,14,![]() .
.
假设所有病人的康复时间相互独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(1)求甲的康复时间不少于14天的概率;
(2)如果![]() ,求甲的康复时间比乙的康复时间长的概率.
,求甲的康复时间比乙的康复时间长的概率.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】从某大学数学系图书室中任选一本书,设![]() {数学书},
{数学书},![]() {中文版的书},
{中文版的书},![]() {2018年后出版的书},问:
{2018年后出版的书},问:
(1)![]() 表示什么事件?
表示什么事件?
(2)在什么条件下,有![]() ?
?
(3)![]() 表示什么意思?
表示什么意思?
(4)如果![]() ,那么是否意味着图书室中的所有的数学书都不是中文版的?
,那么是否意味着图书室中的所有的数学书都不是中文版的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为﹣4,且关于x的不等式f(x)≤0的解集为{x|﹣1≤x≤3,x∈R}.
(1)求函数f(x)的解析式;
(2)求函数g(x)![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,市电视台举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确将给该选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率均为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() (
(![]() )的概率;
)的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年某市政府为了有效改善市区道路交通拥堵状况出台了一系列的改善措施.其中市区公交站点重新布局和建设作为重点项目.市政府相关部门根据交通拥堵情况制定了“市区公交站点重新布局方案”,现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在市区的各公交站点随机抽取若干市民对该“方案”进行评分,并将结果绘制成如图所示的频率分布直方图.相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分,![]() 内认定为满意,不低于
内认定为满意,不低于![]() 分认定为非常满意;③市民对公交站点布局的满意率不低于
分认定为非常满意;③市民对公交站点布局的满意率不低于![]() 即可启用该“方案”;④用样本的频率代替概率.
即可启用该“方案”;④用样本的频率代替概率.

(1)从该市市民中随机抽取![]() 人,求恰有
人,求恰有![]() 人非常满意该“方案”的概率;并根据所学统计学知识判断该市是否启用该“方案”,说明理由;
人非常满意该“方案”的概率;并根据所学统计学知识判断该市是否启用该“方案”,说明理由;
(2)已知在评分低于![]() 分的被调查者中,老年人占
分的被调查者中,老年人占![]() ,现从评分低于
,现从评分低于![]() 分的被调查者中按年龄分层抽取
分的被调查者中按年龄分层抽取![]() 人以便了解不满意的原因,并从中抽取
人以便了解不满意的原因,并从中抽取![]() 人担任群众监督员,记
人担任群众监督员,记![]() 为群众监督员中老年人的人数,求随机变量
为群众监督员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,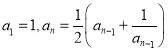 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com