分析:(法一)
( I)由异面直线所成角的定义,考虑AB∥A
1B
1,∠BAC是A
1B
1与AC所成的角.然后在直角三角形ABC中可求∠BAC
(II)由AA
1⊥平面ABC,考虑取AC的中点E,则DE∥AA
1.从而可得DE⊥平面ABC.利用三垂线定理可得BD⊥AC,同理可证BD⊥B
1C,结论可证.
(III)利用定义法:考虑到AB=BB
1,故取AB
1中点F,连接CF,BF可得BF⊥AB
1,由已知可知AC=BC
1同理可得CF⊥AB
1.
则∠BFC为二面角C-AB
1-B的平面角,在Rt△BFC中求解即可
(法二)
(I)同法一
(II)分别以BA、BC、BB
1为x轴、y轴、Z轴建立空间直角坐标系B-xyz,)要证明BD⊥平面AB
1C只有证明
BD⊥AC,BD⊥AB
1,利用向量的知识转化为证明
•=0① • =0②,通过证明①②即可
(III)由题意可得
是平面ABB
1的一个法向量,
是平面AB
1C的一个法向量,代入公式
cosθ=可求.
解答: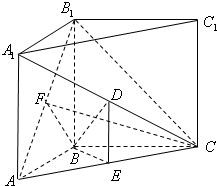
解:法一:(I)在直三棱柱ABC-A
1B
1C
1中,A
1B
1∥AB.
∴∠BAC是A
1B
1与AC所成的角.(2分)
在Rt△ABC中,AB=BC,∠ABC=90°,∴∠BAC=45°.(3分)
∴A
1B
1与AC所成角为45°.(4分)
(II)取AC中点E,连接DE,BE,∵D是A
1C的中点,则DE∥AA
1.
∵AA
1⊥平面ABC,∴DE⊥平面ABC.
则BE是BD在平面ABC内的射影.(6分)
∵AB=BC,∴BE⊥AC.∴BD⊥AC.(7分)
同理可证BD⊥B
1C.(8分)
又AC∩B
1C=C,∴BD⊥平面AB
1C.(9分)
(III)取AB
1中点F,连接CF,BF,(10分)
AB=BB
1,∴BF⊥AB
1∵
AC=B1C=,∴CF⊥AB
1.
则∠BFC为二面角C-AB
1-B的平面角.(12分)
在Rt△BFC中,
BF=,BC=1,∠FBC=90°,
则
tanBFC=.(13分)
∴∠BFC=
arctan.(14分)
即二面角C-AB
1-B的大小为
arctan.
法二:(I)同法一.
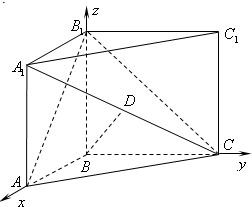
(II)建立空间直角坐标系B-xyz,如图,
则B(0,0,0),A(1,0,0),C(0,1,0),B
1(0,0,1),A
1(1,0,1),D(
,,).(6分)
则
=(,,),
=(-1,1,0),=(-1,0,1).∴
•=0,•=0.(8分)
∴BD⊥AC,BD⊥AB
1,且AC∩AB
1=A.∴BD⊥平面AB
1C.(9分)
(III)∵BC⊥BB
1,BC⊥AB,AB∩BB
1=B,∴BC⊥平面ABB
1.
∴
=(0,1,0)是平面ABB
1的法向量.(11分)
由(II)可知
=(,,)是平面AB
1C的法向量.
cos<,>===.(13分)
即二面角C-AB
1-B的大小为
arccos.(14分)
点评:本小题主要考查空间线面关系中的垂直关系:利用直线与平面垂直的判定定理证明线面垂直的运用;异面直线所成的角的求解,要注意异面直线成角的范围:
(0,];二面角的度量:二面角的平面角的作法①空间向量法,转化为求两个法向量的夹角的求解②定义法,利用空间向量的知识解决几何中的量,考查空间想象能力、推理论证能力和运算求解能力

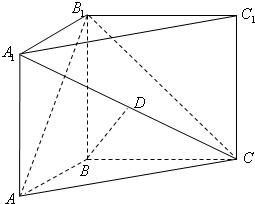 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,点D是A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,点D是A1C的中点. 解:法一:(I)在直三棱柱ABC-A1B1C1中,A1B1∥AB.
解:法一:(I)在直三棱柱ABC-A1B1C1中,A1B1∥AB. (II)建立空间直角坐标系B-xyz,如图,
(II)建立空间直角坐标系B-xyz,如图,





