解:(1)①当0<x≤3时,F在边AC上,
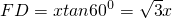
,
∴
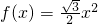
;
当3<x≤5时,F在边BC上,
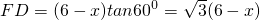
,
∴

∴

②当0<x≤2时,F、G都在边AC上,
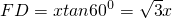
,
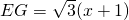
∴

;
当2<x≤3时,F在边AC上,G在边BC上,
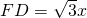
,
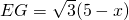
∴
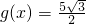
;
当3<x≤5时,F、G都在边BC上,
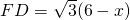
,
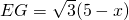
∴
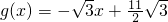
∴
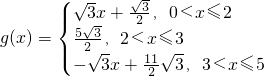
(2)
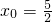
①当
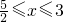
时,
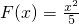
,
∴
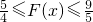
②当3≤x≤5时,
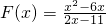
,
∵
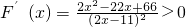
∴
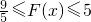
∴F(x)的取值范围为
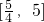
.
分析:(1)当0<x≤3时,F在边AC上,当3<x≤5时,F在边BC上,分别求出△ADF面积即可得到函数f(x)的表达式,当0<x≤2时,F、G都在边AC上,当2<x≤3时,F在边AC上,G在边BC上,当3<x≤5时,F、G都在边BC上分别求出由DE,EG,GF,FD围成的平面图形面积即可得到g(x)的表达式;
(2)根据四边形DEGF为矩形求出x
0,讨论x求出F(x)的解析式,然后根据函数的单调性可求出函数F(x)的取值范围.
点评:本题主要考查了函数模型的选择与应用,以及利用导数研究函数的值域,同时考查了分类讨论的数学思想,属于中档题.

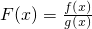 ,求函数F(x)的取值范围.
,求函数F(x)的取值范围.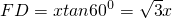 ,
,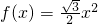 ;
;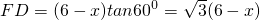 ,
,

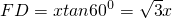 ,
,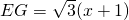
 ;
;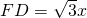 ,
,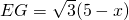
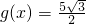 ;
;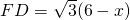 ,
,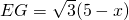
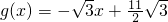
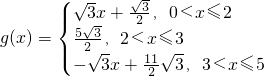
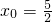
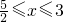 时,
时,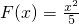 ,
,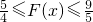
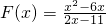 ,
,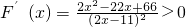
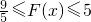
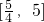 .
.

 阅读快车系列答案
阅读快车系列答案