
【题目】已知函数f(x)=ax﹣lnx(a∈R).
(1)当a=1时,求f(x)的最小值;
(2)若存在x∈[1,3],使 ![]() +lnx=2成立,求a的取值范围;
+lnx=2成立,求a的取值范围;
(3)若对任意的x∈[1,+∞),有f(x)≥f( ![]() )成立,求a的取值范围.
)成立,求a的取值范围.
【答案】
(1)解:f(x)=x﹣lnx(x>0)的导数为f′(x)=1﹣ ![]() =
= ![]() ,
,
当x>1时,f′(x)>0,f(x)递增;当0<x<1时,f′(x)>0,f(x)递减.
即有f(x)在x=1处取得极小值,也为最小值,且为1
(2)解:存在x∈[1,3],使 ![]() +lnx=2成立,
+lnx=2成立,
即为 ![]() =2﹣lnx,
=2﹣lnx,
即有a= ![]() ,
,
设g(x)= ![]() ,x∈[1,3],
,x∈[1,3],
则g′(x)=(1﹣lnx)(1+ ![]() ),
),
当1<x<e时,g′(x)>0,g(x)递增;当e<x<3时,g′(x)<0,g(x)递减.
则g(x)在x=e处取得极大值,且为最大值e+ ![]() ;
;
g(1)=2,g(3)=3(2﹣ln3)+ ![]() >2,
>2,
则a的取值范围是[2,e+ ![]() ]
]
(3)解:若对任意的x∈[1,+∞),有f(x)≥f( ![]() )成立,
)成立,
即为ax﹣lnx≥ ![]() ﹣ln
﹣ln ![]() ,
,
即有a(x﹣ ![]() )≥2lnx,x≥1,
)≥2lnx,x≥1,
令F(x)=a(x﹣ ![]() )﹣2lnx,x≥1,
)﹣2lnx,x≥1,
F′(x)=a(1+ ![]() )﹣
)﹣ ![]() ,
,
当x=1时,原不等式显然成立;
当x>1时,由题意可得F′(x)≥0在(1,+∞)恒成立,
即有a(1+ ![]() )﹣
)﹣ ![]() ≥0,
≥0,
即a≥ ![]() ,由
,由 ![]() =
= ![]() <
< 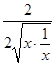 =1,
=1,
则a≥1.
综上可得a的取值范围是[1,+∞)
【解析】(1)求得f(x)的导数,求得单调区间,可得f(x)的极小值,也为最小值;(2)由题意可得a= ![]() ,设g(x)=
,设g(x)= ![]() ,x∈[1,3],求出导数和单调区间,极值和最值,即可得到所求a的范围;(3)由题意可得ax﹣lnx≥
,x∈[1,3],求出导数和单调区间,极值和最值,即可得到所求a的范围;(3)由题意可得ax﹣lnx≥ ![]() ﹣ln
﹣ln ![]() ,即有a(x﹣
,即有a(x﹣ ![]() )≥2lnx,x≥1,令F(x)=a(x﹣
)≥2lnx,x≥1,令F(x)=a(x﹣ ![]() )﹣2lnx,x≥1,求出导数,讨论x=1,x>1时,F(x)递增,运用分离参数和基本不等式,即可得到a的范围.
)﹣2lnx,x≥1,求出导数,讨论x=1,x>1时,F(x)递增,运用分离参数和基本不等式,即可得到a的范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:实数x满足x2﹣5ax+4a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,an+1= ![]() (n∈N+).
(n∈N+).
(1)计算a2 , a3 , a4 , 并猜测出{an}的通项公式;
(2)用数学归纳法证明(1)中你的猜测.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是方程
是方程![]()
![]() 的两个不等实根,函数
的两个不等实根,函数![]() 的定义域为
的定义域为![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最值;
的最值;
(2)试判断函数![]() 在区间
在区间![]() 的单调性;
的单调性;
(3)设![]() ,试证明:对于
,试证明:对于![]() ,若
,若![]() ,则
,则 .
.
(参考公式: ![]() ,当且仅当
,当且仅当![]() 时等号成立)
时等号成立)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足 ![]() =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则该数列首项a1的取值范围是( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则该数列首项a1的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为 ![]() ,则该产品投放市场第几天的销售额最高?最高为多少千元?
,则该产品投放市场第几天的销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:
(1)顶点C的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,A(1,3),BC边所在的直线方程为y﹣1=0,AB边上的中线所在的直线方程为x﹣3y+4=0. (Ⅰ)求B,C点的坐标;
(Ⅱ)求△ABC的外接圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车,购车费用是10万元,每年使用的保险费、养路费、汽车费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万元,问这种汽车使用多少年时,它的平均费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com