
已知椭圆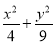 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且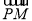 =2
=2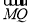 ,点M的轨迹为C.
,点M的轨迹为C.
(1)求曲线C的方程;
(2)过点D(0,-2)作直线l与曲线C交于A、B两点,设N是过点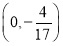 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足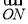 =
=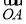 +
+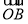 (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程.
(1)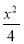 +y2=1(2)y=±2x-2.
+y2=1(2)y=±2x-2.
【解析】(1)设点M(x,y)是曲线C上任意一点,
∵PM⊥x轴,且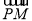 =2
=2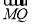 ,
,
所以点P的坐标为(x,3y),
又点P在椭圆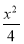 +
+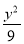 =1上,所以
=1上,所以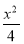 +
+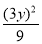 =1,
=1,
因此曲线C的方程是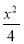 +y2=1.
+y2=1.
(2)当直线l的斜率不存在时,显然不满足条件,所以设直线l的方程为y=kx-2,直线l与椭圆交于A(x1,y1),B(x2,y2)两点.
由 得(1+4k2)x2-16kx+12=0,
得(1+4k2)x2-16kx+12=0,
依题意Δ=(16k)2-48(1+4k2)>0,得k2>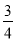 (*),
(*),
此时x1+x2=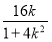 ,x1x2=
,x1x2=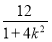 .
.
因为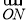 =
=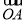 +
+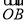 ,所以四边形OANB为平行四边形.
,所以四边形OANB为平行四边形.
又四边形OANB是矩形,所以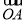 ·
·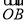 =0,
=0,
即x1x2+y1y2=x1x2+k2x1x2-2k(x1+x2)+4=(1+k2)x1x2-2k(x1+x2)+4=0,
∴(1+k2)·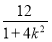 -2k·
-2k·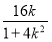 +4=0,
+4=0,
解之得k2=4,∴k=±2.满足(*)式.
设N(x0,y0),由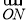 =
=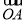 +
+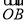 ,得
,得
y0=y1+y2=k(x1+x2)-4=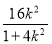 -4=-
-4=-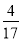 ,
,
从而点N在直线y=-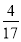 上,满足题设,
上,满足题设,
故直线l的方程为y=±2x-2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(解析版) 题型:解答题
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(解析版) 题型:填空题
如图所示,图(2)中实线围成的部分是长方体(图(1))的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点.它落在长方体的平面展开图内的概率是 ,则此长方体的体积是________.
,则此长方体的体积是________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-1练习卷(解析版) 题型:选择题
在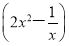 5的二项展开式中,x的系数为( ).
5的二项展开式中,x的系数为( ).
A.10 B.-10 C.40 D.-40
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-3练习卷(解析版) 题型:选择题
已知双曲线C1: =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为 ( ).
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为 ( ).
A.x2= y B.x2=
y B.x2= y C.x2=8y D.x2=16y
y C.x2=8y D.x2=16y
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(解析版) 题型:填空题
已知抛物线y2=8x的准线过双曲线 =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-1练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小是( ).

A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(解析版) 题型:填空题
已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com