数列
满足
，
．
（Ⅰ）求
、
、
；
（Ⅱ）求
的表达式；
（Ⅲ）令
，求
．
（Ⅰ）
、
、
；
（Ⅱ）
（Ⅲ）
解析试题分析：（Ⅰ）由递推公式即可求出、、；（Ⅱ）方法一：猜想出通项公式，然后用数学归纳法证明；方法二：由递推公式可以构造等比数列，借助等比数列可以求出通项公式；方法二：由递推公式可以构造等差数列，借助等差数列可以求出通项公式；.
（Ⅰ）由递推公式：、、； 3分
（Ⅱ）方法一：猜想：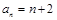
，下面用数学归纳法证明：
① ，猜想成立；
② 假设
时，
，
则
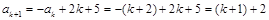，即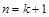
时猜想成立，
综合①②，由数学归纳法原理知：． 8分
方法二：由得
，
所以：． 8分
方法三：由得：
，两式作差得：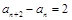
，
于是
是首项，公差为
的等差数列，那么
，
且
是首项，公差为的等差数列，那么
，
综上可知：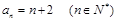
． 8分
（Ⅲ）
10分
． 12分.
考点：归纳推理、数学归纳法、数列求和.
科目：高中数学 来源： 题型：解答题
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)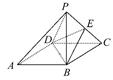
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，在三棱锥S－ABC中，SA⊥SB，SB⊥SC，SA⊥SC，且SA、SB、
SC和底面ABC，所成的角分别为α1、α2、α3，三侧面SBC，SAC，SAB的面积分别为S1，S2，S3，类比三角形中的正弦定理，给出空间情形的一个猜想．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（Ⅰ）若函数
在其定义域上为单调函数,求
的取值范围；
（Ⅱ）若函数的图像在
处的切线的斜率为0，
，已知
求证：
（Ⅲ）在（2）的条件下，试比较
与
的大小，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(
)
均为实数，且
，
，
求证：
成立．
.
…
＝
都成立．
是虚数单位，则复数
的虚部是( ) 
: