
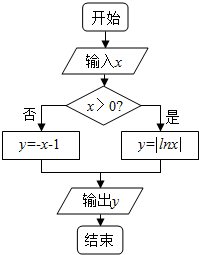
 给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2.
给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2. 分析 根据流程图,得出该程序运行后执行的是y=$\left\{\begin{array}{l}{|lnx|,x>0}\\{-x-1,x≤0}\end{array}\right.$,令y=x,求出方程解的个数即可.
解答  解:根据流程图,得
解:根据流程图,得
该程序运行后执行的是y=$\left\{\begin{array}{l}{|lnx|,x>0}\\{-x-1,x≤0}\end{array}\right.$,
要使输入的x的值与输出的y的值相等,
需要$\left\{\begin{array}{l}{|lnx|=x,x>0①}\\{-x-1=x,x≤0②}\end{array}\right.$,
解①得lnx=±x,结合函数的图象知,
该方程有1个实数解;
解②得x=-$\frac{1}{2}$;
所以,这样的x值的个数是2.
故答案为:2.
点评 本题考查了能根据程序框图的流程得到框图的功能应用问题,也考查了函数零点的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )| A. | 12-2$\sqrt{2}$ | B. | 12+2$\sqrt{2}$ | C. | 10+2$\sqrt{5}$ | D. | 10-2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 0 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 不喜欢数学课程 | 喜欢数学课程 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总 | 75 | 25 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有90%以上的把握认为“性别与是否喜欢数学课程有关” | |
| B. | 有90%以上的把握认为“性别与是否喜欢数学课程没有关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程没有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | -$\frac{7}{8}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com