
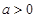 ,函数
,函数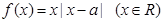 .
.
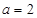 时,画出函数
时,画出函数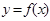 的大致图像;
的大致图像;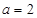 时,根据图像写出函数
时,根据图像写出函数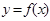 的单调减区间,并用定义证明你的结论;
的单调减区间,并用定义证明你的结论;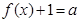 解的个数.
解的个数.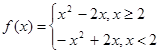 ,作出图象;
,作出图象;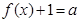 的解得个数等价于函数
的解得个数等价于函数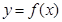 的图像与直线
的图像与直线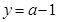 的交点个数.即函数
的交点个数.即函数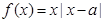 的图象与直线
的图象与直线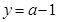 的交点个数.
的交点个数.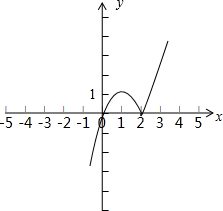 3分
3分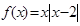 单调递减区间:
单调递减区间: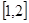 4分
4分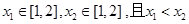
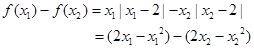
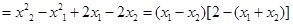 5分
5分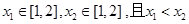 ,所以
,所以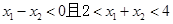
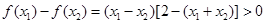 ,即
,即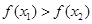 6分
6分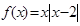 在
在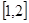 上是单调递减函数 7分
上是单调递减函数 7分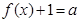 的解得个数等价于函数
的解得个数等价于函数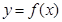 的图像与直线
的图像与直线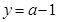 的交点个数.即函数
的交点个数.即函数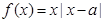 的图象与直线
的图象与直线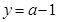 的交点个数
的交点个数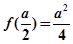 ,注意到
,注意到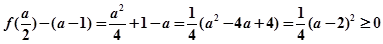 ,
,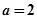 时,上式等号成立,借助图像知 8分
时,上式等号成立,借助图像知 8分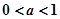 时,函数
时,函数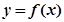 的图像与直线
的图像与直线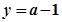 有1个交点; 9分
有1个交点; 9分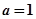 ,
,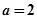 时,函数
时,函数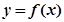 的图像与直线
的图像与直线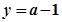 有2个交点; 10分
有2个交点; 10分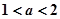 ,
,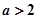 时,函数
时,函数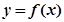 的图像与直线
的图像与直线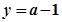 有3个交点;12分.
有3个交点;12分.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com