练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若命题“$x∈R,x2＋ax＋1＜0”是真命题，则实数a的取值范围为  。

    a∈(－∞，－2)∪(2，＋∞)

    解析试题分析：∵命命题“存在实数x，使x2＋ax＋1＜0”的否定是假命题，∴原命题为真命题，即“存在实数x，使x2＋ax＋1＜0”为真命题，∴△=a2-4＞0=∴a＜-2或a＞2，故答案为：a＜-2或a＞2.
    考点：命题的真假判断与应用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

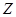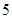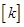    在整数集中，被除所得余数为的所有整数组成一个“类”，记为，则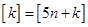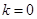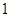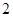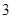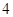，、、、、，则下列结论正确的是_____________.
    ①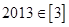              ②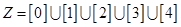
    ③“整数、属于同一‘类’”的充要条件是“”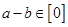
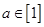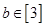    ④命题“整数、满足，，则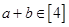”的原命题与逆命题都为真命题.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    命题“"x∈N，x2≠x”的否定是     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    (1)命题“若a＞b，则2a＞2b－1”的否命题为____________________________；
    (2)命题：“若x2＋x－m＝0没有实根，则m≤0”是____(填“真”或“假”)命题；
    (3)命题p：“有些三角形是等腰三角形”，则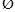p是____________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若a、b为实数，则“0<ab<1”是“b<”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    命题“若，则”的否命题是：__________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在命题p的四种形式(原命题、逆命题、否命题、逆否命题)中，真命题的个数记为f(p)，已知命题p：“若两条直线l1：a1x＋b1y＋c1＝0，l2：a2x＋b2y＋c2＝0平行，则a1b2－a2b1＝0”．那么f(p)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在△ABC中，角A，B，C所对的边分别为a，b，c，有下列命题：①在△ABC中，A＞B是sinA＞sinB的充分不必要条件；②在△ABC中，A＞B是cosA＜cosB的充要条件；③在△ABC中，A＞B是tanA＞tanB的必要不充分条件．其中正确命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    有三个命题:(1)“若x+y=0,则x,y互为相反数”的逆命题.
    (2)“若a>b,则a2>b2”的逆否命题.
    (3)“若x≤-3,则x2+x-6>0”的否命题.
    其中真命题的个数为　　　　.

    查看答案和解析>>

    同步练习册答案