
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望.
(1) ;(2)分布列详见解析;
;(2)分布列详见解析; .
.
【解析】
试题分析:本题主要考查独立事件、离散型随机变量的分布列和数学期望等基础知识,同时考查考生的分析问题解决问题的能力、运算求解能力. 第一问,先利用已知直接得出四个入口拥堵的概率,再结合独立事件的概率公式计算该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;第二问,结合第一问的计算方法,分别计算出 、
、 、
、 、
、 、
、 的值,列出分布列,利用
的值,列出分布列,利用 计算数学期望.
计算数学期望.
试题解析:(Ⅰ)设东西南北四个主干道入口发生拥堵分别为事件A,B,C,D.
则 ,
, ,
, ,
,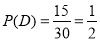 .
.
设一天恰有三个入口发生拥堵为事件M,则
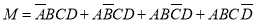 .
.
则 . 5分
. 5分
(Ⅱ)ξ的可能取值为0,1,2,3,4.
 ,
,
 ,
,
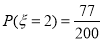 ,
,
 ,
,
 .
.
ξ的分布列为:
ξ | 0 | 1 | 2 | 3 | 4 |
p |
|
|
|
|
|
E()=0× +1×
+1× +2×
+2×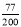 +3×
+3× +4×
+4× =
= =
=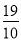 . 12分
. 12分
考点:独立事件、离散型随机变量的分布列和数学期望.


科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试文科数学试卷(解析版) 题型:解答题
如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且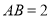 km,
km,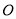 为圆心,
为圆心,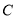 为圆周上靠近
为圆周上靠近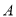 的一点,
的一点,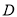 为圆周上靠近
为圆周上靠近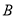 的一点,且
的一点,且 ∥
∥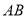 .现在准备从
.现在准备从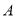 经过
经过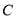 到
到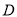 建造一条观光路线,其中
建造一条观光路线,其中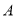 到
到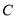 是圆弧
是圆弧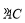 ,
,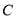 到
到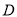 是线段
是线段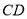 .设
.设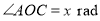 ,观光路线总长为
,观光路线总长为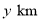 .
.

(1)求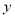 关于
关于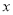 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
设函数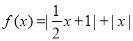
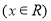 的最小值为a.
的最小值为a.
(1)求a;
(2)已知两个正数m,n满足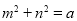 ,求
,求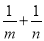 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A.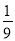 B.
B.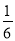 C.
C.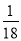 D.
D.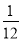
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
设函数
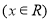 的最小值为a.
的最小值为a.
(1)求a;
(2)已知两个正数m,n满足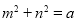 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com