
分析 (1)利用抛物线C:y2=2px(p>0)的焦点F(1,0),可得抛物线C的方程;
(2)分类讨论,设出直线的方程,与抛物线方程联立,利用韦达定理,结合斜率公式,可求直线方程,即可得出结论.
解答 (1)解:因为抛物线y2=2px(p>0)的焦点坐标为(1,0),
所以$\frac{p}{2}$=1,所以p=2.
所以抛物线C的方程为y2=4x.
(2)证明:①当直线AB的斜率不存在时,设A($\frac{{t}^{2}}{4}$,t),B($\frac{{t}^{2}}{4}$,-t),
因为直线OA,OB的斜率之积为-$\frac{1}{3}$,所以$\frac{t}{\frac{{t}^{2}}{4}}•\frac{-t}{\frac{{t}^{2}}{4}}$=-$\frac{1}{3}$,化简得t2=48.
所以(12,t),B(12,-t),此时直线AB的方程为x=12.----------------(7分)
②当直线AB的斜率存在时,设直线的方程为y=kx+b,A(xA,yA),B(xB,yB)
联立方程,化简得ky2-4y+4b=0.------------------(9分)
根据韦达定理得到yAyB=$\frac{4b}{k}$,
因为直线OA,OB的斜率之积为-$\frac{1}{3}$,所以得到xAxB+3yAyB=0.--------------------(11分)
得到$\frac{{{y}_{A}}^{2}}{4}•\frac{{{y}_{B}}^{2}}{4}$+2yAyB=0,
化简得到yAyB=0(舍)或yAyB=-48.--------------------(12分)
又因为yAyB=$\frac{4b}{k}$=-48,b=-12k,
所以y=kx-12k,即y=k(x-12).
综上所述,直线AB过定点(12,0).
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
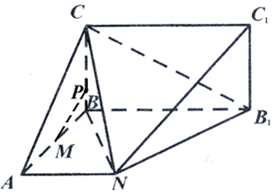 如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.
如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com