练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．下列结论不正确的是（　　）
    A．$\left.\begin{array}{l}{A∈α}\\{a?α}\end{array}\right\}$⇒A∈αB．$\left.\begin{array}{l}{A∈α，A∈β}\\{α∩β=α}\end{array}\right\}$⇒A∈α
    C．$\left.\begin{array}{l}{A∈α}\\{A∈β}\end{array}\right\}$⇒α∩β=AD．$\left.\begin{array}{l}{A∈α}\\{B∈α}\end{array}\right\}$⇒AB?α

    分析 根据题意，对四个选项进行分析、判断，即可得出正确的答案．

    解答 解：对于A，A∈α⇒A∈α，命题正确；
    对于B，$\left.\begin{array}{l}{A∈α，A∈β}\\{α∩β=a}\end{array}\right\}$⇒A∈α∩β=a，命题正确；
    对于C，α∩β是一条直线，不是一个点，∴命题错误；
    对于D，$\left.\begin{array}{l}{A∈α}\\{B∈α}\end{array}\right\}$⇒AB?平面α，命题正确．
    故选：C．

    点评 本题考查了几何符号语言与空间想象能力的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

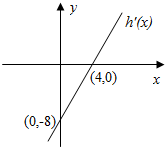    17．已知二次函数h（x）=ax2+bx+2，其导函数y=h′（x）的图象如图，f（x）=6lnx+h（x）．
    （1）求函数f（x）的解析式；
    （2）若函数f（x）在区间$（{1，m+\frac{1}{2}}）$上是单调函数，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知斜率为2的直线经过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的右焦点F1，与椭圆相交于A、B两点，求弦AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．数列{an}中，为递增等比数列，a2=9，a1+a3=30．
    （1）求{an}；
    （2）数列{2n•an}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知曲线f（x）=$\frac{1}{3}$x3+ax2+3x-$\frac{5}{6}$（a＞-2）在点（1，f（1））处的切线l与坐标轴转成的三角形的面积为$\frac{2}{5}$．
    （1）求实数a的值；
    （2）若a＞0，且对?x1，x2∈[-1，1]，2${\;}^{f（{x}_{1}）-f（{x}_{2}）-6}$＜$\root{3}{m}$恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知正三棱锥底面的边长是$\frac{15}{2}$，高与侧棱的夹角为60°，求它的侧面积和表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若不等式2x2+（1-a）y2≥（3+a）xy（x＞0，y＞0）恒成立．则实数a的最大值为4$\sqrt{3}$-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数f（x）（x∈R）关于（-$\frac{3}{4}$，0）对称，且f（x）=-f（x+$\frac{3}{2}$）则下列结论：（1）f（x）的最小正周期是3，（2）f（x）是偶函数，（3）f（x）关于x=$\frac{3}{2}$对称，（4）f（x）关于（$\frac{9}{4}$，0）对称，正确的有（1）（2）（3）（4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知等比数列{an}的前n项和为Sn，且$\frac{{S}_{8}-{S}_{6}}{{S}_{6}-{S}_{4}}$=$\sqrt{2}$，则$\frac{{a}_{8}}{{a}_{4}}$=（　　）
    A．$\sqrt{2}$B．2C．4D．16

    查看答案和解析>>

    同步练习册答案