
| 2 |
| 3 |
| 2 |
| 3 |
科目:高中数学 来源: 题型:
| 1 |
| b |
| 1 |
| a |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省泰州市泰兴市高一(下)期末数学试卷(解析版) 题型:填空题
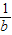 ,
,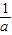 ),则称这两个不等式为对偶不等式.如果不等式x2-4
),则称这两个不等式为对偶不等式.如果不等式x2-4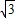 x•cosθ+2<0与不等式2x2-4x•sinθ+1<0为对偶不等式,且θ∈(
x•cosθ+2<0与不等式2x2-4x•sinθ+1<0为对偶不等式,且θ∈(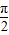 ,π),则θ= .
,π),则θ= .查看答案和解析>>
科目:高中数学 来源:0110 期中题 题型:填空题
 在[-1,∞)上是减函数,则实数a的取值范围是(-8,-6];
在[-1,∞)上是减函数,则实数a的取值范围是(-8,-6];查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法中:
①若f(x)=ax2+(2a+b)x+2(其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②f(x)表示 -2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;
③如果![]() 在[-1,∞
在[-1,∞![]() 上是减函数,则实数a的取值范围是(-8,-6
上是减函数,则实数a的取值范围是(-8,-6![]() ;
;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足
f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.
其中正确说法的序号是____________________(注:把你认为是正确的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com