
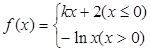 ,则下列关于
,则下列关于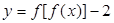 的零点个数判断正确的是( )
的零点个数判断正确的是( )
| A.当k=0时,有无数个零点 | B.当k<0时,有3个零点 |
| C.当k>0时,有3个零点 | D.无论k取何值,都有4个零点 |
A
解析试题分析:因为函数f(x)为分段函数,函数y=f(f(x))-2为复合函数,故需要分类讨论,确定函数y=f(f(x))+1的解析式,从而可得函数y=f(f(x))-2的零点个数;解:分四种情况讨论.(1)0<x<1时,lnx<0,∴y=f(f(x))+1=-ln(-lnx)+1,此时的零点为x=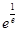 >1;(2)x>1时,lnx>0,∴y=f(f(x))+1=klnx+1,则k>0时,有一个零点,k<0时,klnx+1>0没有零点;(3)若x<0,kx+2≤0时,y=f(f(x))+1=k2x+k+1,则k>0时,kx≤-2,k2x≤-k,可得k2x+k≤0,y有一个零点,若k<0时,则k2x+k≥0,y没有零点,(4)若x<0,kx+2>0时,y=f(f(x))+1=ln(kx+1)+1,则k>0时,即y=0可得kx+2=
>1;(2)x>1时,lnx>0,∴y=f(f(x))+1=klnx+1,则k>0时,有一个零点,k<0时,klnx+1>0没有零点;(3)若x<0,kx+2≤0时,y=f(f(x))+1=k2x+k+1,则k>0时,kx≤-2,k2x≤-k,可得k2x+k≤0,y有一个零点,若k<0时,则k2x+k≥0,y没有零点,(4)若x<0,kx+2>0时,y=f(f(x))+1=ln(kx+1)+1,则k>0时,即y=0可得kx+2=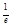 ,y有一个零点,k<0时kx>0,y没有零点,综上可知,当k>0时,有4个零点;当k<0时,有1个零点,故选A;k=0,y=f(f(x))-2,有无数个零点,故选A.
,y有一个零点,k<0时kx>0,y没有零点,综上可知,当k>0时,有4个零点;当k<0时,有1个零点,故选A;k=0,y=f(f(x))-2,有无数个零点,故选A.
考点:复合函数的零点
点评:本题考查分段函数,考查复合函数的零点,解题的关键是分类讨论确定函数y=f(f(x))+1的解析式,考查学生的分析能力,是一道中档题;


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:单选题
下列说法中,不正确的是
A.点 为函数 为函数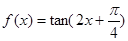 的一个对称中心 的一个对称中心 |
B.设回归直线方程为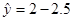 x,当变量x增加一个单位时,y大约减少2.5个单位 x,当变量x增加一个单位时,y大约减少2.5个单位 |
| C.命题“在△ABC中,若sinA="sin" B,则△ABC为等腰三角形”的逆否命题为真命题 |
D.对于命题p:“ ”则 ”则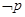 “ “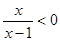 ” ” |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知y=f(x)是奇函数,当x>0时,f(x)=2x(1-x),当x<0时f(x)应该等于 ( )
| A.–2x(1-x) | B.2x(1-x) | C.–2x(1+x) | D.2x(1+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
函数f(x)在定义域R内可导,若f(x)=f(4-x),且当x∈(-∞,2)时,(x-2)·f′(x)<0,设a=f(4),b=f(1), c=f(-1),则a,b,c由小到大排列为 ( )
| A.a<b<c | B.a<c<b | C.c<b<a | D.c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com