
(11分)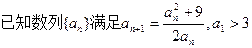
(1)求证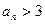 ;
;
(2)比较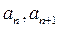 的大小,并证明
的大小,并证明
(3)是否存在 证明你的结论。
证明你的结论。
当a1>3时,用数学归纳法证明an>3.
(1)当n=1时不等式成立.
(2)假设当n=k时不等式成立,即ak>3,则
ak+1=>=3,
即当n=k+1时不等式仍成立.
根据(1)和(2),对任何n∈N*,都有an>3.………………………………4分
∵an+1-an=-an=<0,∴an+1<an,n∈N*,………… 7分
(Ⅱ)假设存在使题设成立的正整数m,则
(am-3)(am+2-3)=(am+1-3)2即(am-3)·=(am+1-3)2,
∴am-3=2am+1,即am-3=,从而am=-3,这不可能.
故不存在m∈N*,使得(am-3)(am+2-3)=(am+1-3)2.…………………… 11分
解析


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本小题满分13分)
设数列![]() 的各项都是正数, 且对任意
的各项都是正数, 且对任意![]() 都有
都有![]() 记
记![]() 为数列
为数列![]() 的前n项和
的前n项和
(1) 求证: ![]() ;(2) 求数列
;(2) 求数列![]() 的通项公式;
的通项公式;
(3) 若![]() (
(![]() 为非零常数,
为非零常数, ![]() ), 问是否存在整数
), 问是否存在整数![]() , 使得对任意
, 使得对任意![]() ,
,
都有![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省高三第三轮适应性考试理科数学试卷(解析版) 题型:解答题
如图,四边形 是圆内接四边形,延长
是圆内接四边形,延长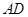 与的延长线
与的延长线 交于点
交于点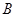 ,且
,且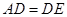 ,
, 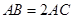 .
.
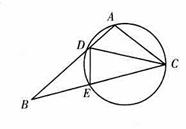
(1)求证: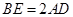 ;
;
(2)当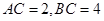 时,求
时,求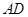 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第四次月考文科数学试卷(解析版) 题型:解答题
一个多面体的直观图和三视图如下:(其中 分别是
分别是 中点)
中点)

(1)求证: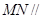 平面
平面 ;
;
(2)求多面体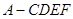 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三12月月考理科数学卷 题型:解答题
(12)如图,四棱锥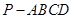 的底面
的底面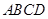 为正方形,
为正方形,
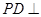 平面
平面 ,
,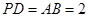 ,
,
 ,
,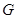 分别为
分别为 ,
,
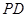 和
和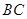 的中点. (1)求证
的中点. (1)求证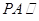 平面
平面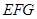 .(2)求异面直线
.(2)求异面直线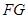 与
与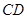 所成角的正切值.
所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com