（本小题12分）设函数y=x
+ax
+bx+c的图像，如图所示，且与y=0在原点相切，若函数的极小值为–4，
（1）求a、b、c的值；
（2）求函数的递减区间。
（1）-3 0 0
（2）函数的单调区间为（0,2）
【解析】解：（1）由图可知函数经过原点（0,0），代入函数得c=0-------------2分
导函数y
=3x
+2ax+b
-----------------------4分
函数图像在原点处与x轴相切，则（0,0）在其导函数图像上，代入得b=0 ------6分
则y= x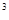
+ax y=3x+2ax，令y=3x+2ax=0，得x=0或x=－
a
由图可知－a>0
--------7分
|
x |
（－∞，0） |
0 |
（0，－ |
－ |
（－ |
|
f |
＋ |
0 |
－ |
0 |
＋ |
|
f(x) |
↗ |
极大值0 |
↘ |
极小值－ |
↗ |
可知极小值为－
+
，故－+=－4，解得a=－3 ------10分
（2）由（1）a=－3,得y=x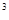－3x,－a=2
由上表显然函数的单调区间为（0,2）（或者表示为[0,2],区间开闭都行-----12分
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2011-2012学年内蒙古呼伦贝尔市高三第四次模拟考试理科数学试卷 题型：解答题
（本小题满分12分）
已知函
的部分图象如图所示：
(1)求
的值；
(2)设
，当
时，求函数
的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
（本小题分A,B类，满分12分，任选一类，若两类都选，以A类记分）
（A类）已知函数
的图象恒过定点
，且点又在函
数
的图象.
（1）求实数
的值； （2）解不等式
；
(3)
有两个不等实根时，求
的取值范围.
（B类）设
是定义在
上的函数，对任意
，恒有
.
⑴求
的值； ⑵求证：为奇函数；
⑶若函数是上的增函数，已知
且
，求的
取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
（本小题满分12分）
已知定理：若“
为常数，
满足
，则函数
的图象关于点
中心对称。”设函数
，定义域为A。
（1）证明：函数
的图象关于点
中心对称；
（2）当
时，求函数值
的取值范围；
（3）对于给定的
，设计构造过程：
，若
，构造过程将继续下去；若
，构造过程都可以无限进行下去，求
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的部分图象如图所示：
的值；
，当
时，求函数
的值域.
的部分图象如图所示：
的值；
，当
时，求函数
的值域．