
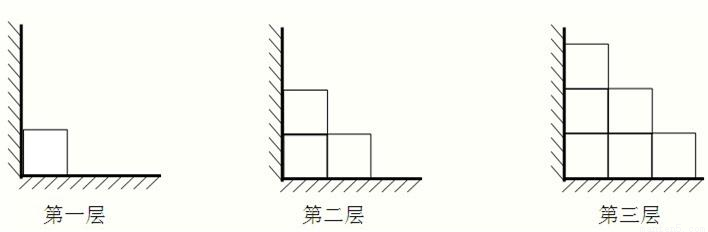
 (n2+n),a10=可求.再利用分组求和法求和即可.
(n2+n),a10=可求.再利用分组求和法求和即可.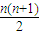 =
= (n2+n)(n≥2),且a1=1也适合.
(n2+n)(n≥2),且a1=1也适合. (12+22+…+102)+
(12+22+…+102)+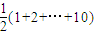
 ×
×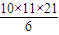 +
+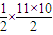 =220.
=220.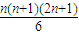 .
. 

科目:高中数学 来源: 题型:
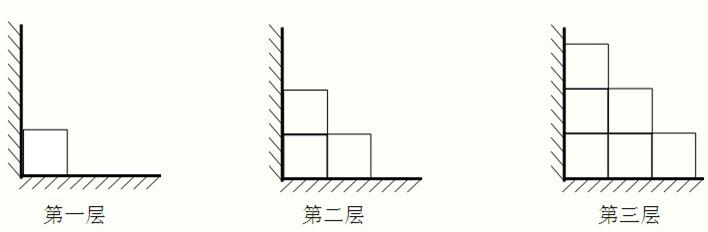
查看答案和解析>>
科目:高中数学 来源: 题型:
;车间地上放有一批大小相同的黄、白两种颜色的乒乓球,黄、白数量之比为1:2,现从车间中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以![]() 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.
(Ⅰ)求![]() 的分布列;(Ⅱ)求
的分布列;(Ⅱ)求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
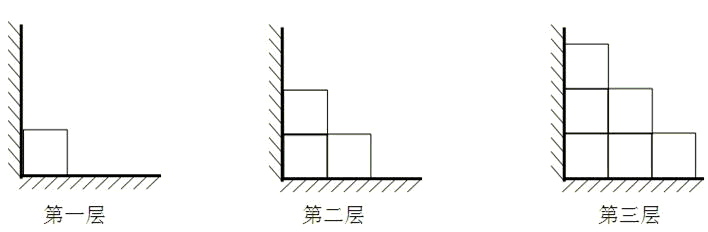
查看答案和解析>>
科目:高中数学 来源:0103 期中题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com