
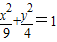 ,则
,则 的取值范围为 .
的取值范围为 . 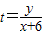 看成是定点A(-6,0)与椭圆
看成是定点A(-6,0)与椭圆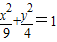 上动点P连线的斜率,且过定点A(-6,0)的直线与椭圆一定有交点,先求出直线与椭圆有交点的特殊情况,即直线与椭圆相切时的t值,其它情况应在两条切线之间,即可求出范围.
上动点P连线的斜率,且过定点A(-6,0)的直线与椭圆一定有交点,先求出直线与椭圆有交点的特殊情况,即直线与椭圆相切时的t值,其它情况应在两条切线之间,即可求出范围.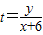 可以斜率,
可以斜率,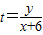 的取值范围为过定点
的取值范围为过定点 +
+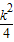 )x2+3k2x+9k2-1=0
)x2+3k2x+9k2-1=0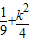 )(9k2-1)=0
)(9k2-1)=0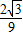 .
.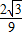 到
到 之间.
之间.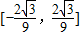
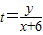 的几何意义,以及直线与椭圆切线求法,求t范围做题时应认真分析,找到切入点.
的几何意义,以及直线与椭圆切线求法,求t范围做题时应认真分析,找到切入点. 

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com