
����Ŀ��һ�����С��Ϸ�Ĺ������£�ÿ����Ϸ����������Σ�ÿ�λ���Ҫô����һ�����֣�Ҫô���������֣�ÿ����Ϸ�������κ���һ�����ֻ��10�֣������������ֻ��20�֣������������ֻ��100�֣�û�г���������۳�200�֣�����ã�200�֣�����ÿ�λ��ij������ֵĸ���Ϊ![]() ���Ҹ��λ����Ƿ���������������
���Ҹ��λ����Ƿ���������������
��1����������Ϸ��������һ�ֳ������ֵĸ����Ƕ��٣�
��2����ÿ����Ϸ��õķ���ΪX����X�ķֲ��м���ѧ������
���𰸡���1��![]() ��(2)������
��(2)������
��������
��1�����ö����¼����ó�P��A1����P��A2����P��A3����P��X����200��![]() �����P��A1A2A3�����ɵó�1��P��A1A2A3����
�����P��A1A2A3�����ɵó�1��P��A1A2A3����
��2��X���ܵ�ȡֵΪ10��20��100����200�����ü��θ��ʹ�ʽ�ó������Ӧ�ĸ��ʣ��ó��ֲ��У�
��1���衰��i����Ϸû�г������֡�Ϊ�¼�Ai��i��1��2��3������
P��A1����P��A2����P��A3����P��X����200��![]() ��
��
���ԡ�������Ϸ��������һ�ֳ������֡��ĸ���Ϊ1��P��A1A2A3����1��![]() ��
��
��ˣ���������Ϸ������һ�ֳ������ֵĸ�����![]() ��
��
��2��X���ܵ�ȡֵΪ10��20��100����200���������⣬��
P��X��10��![]() ��
��![]() ��1����1
��1����1![]() ��2
��2![]() ��
��
P��X��20��![]() ��
��![]() ��2����1
��2����1![]() ��1
��1![]() ��
��
P��X��100��![]() ��
��![]() ��3����1
��3����1![]() ��0
��0![]() ��
��
P��X����200��![]() ��
��![]() ��0����1
��0����1![]() ��3
��3![]() ��
��
��X�ķֲ���Ϊ��
X | 10 | 20 | 100 | ��200 |
P |
|
|
|
|
E(��)��![]() .
.


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij������![]() �У��ı���
�У��ı���![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �������Σ�
�������Σ� ![]() ��ֱ�����Σ�
��ֱ�����Σ� ![]() ��ֱ�ǣ�
��ֱ�ǣ� ![]() ��
�� ![]() ����
����![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ�
Ϊֱ�Ƕ���ĵ���ֱ�������Σ� ![]() .
.
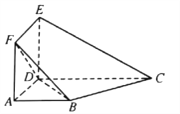
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵ������ǵ�����ֵ.
���ɵ������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��ex(x2��ax��a)������a�dz�����
(1)��a��1ʱ��������y��f(x)�ڵ�(1��f(1))�������߷��̣�
(2)������ʵ��k��ʹ�ù���x�ķ���f(x)��k��[0������)������������ȵ�ʵ��������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ֪��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������ԭ��
Ϊ����������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���ᣬ����������ϵ������
���������Ϊ���ᣬ����������ϵ������![]() �ļ����귽��
�ļ����귽��![]() .
.
��1����ֱ��![]() ����ͨ���̼�����
����ͨ���̼�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��������![]() ��
��![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ����
����![]() ��������Ľ���Ϊ
��������Ľ���Ϊ![]() ����ֱ��
����ֱ��![]() ��
��![]() �ֳɵ������ֵ������.
�ֳɵ������ֵ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������к����Ķ������ֵ��д���䵥������.
��1��![]() ��
��
��2��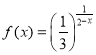 ��
��
��3��![]() ��
��
��4��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У���1��ʼ���ΰ����¹���ijЩ����Ⱦ�ɺ�ɫ����Ⱦ1����Ⱦ3��ż��2��4��6����Ⱦ6�������ڽ���5����������7��9��11��13��15����Ⱦ15�������ڽ���7������ż��16��18��20��22��24��26��28����Ⱦ�˺����ڽ���9����������29��31��![]() ��45�����˹���һֱȾ��ȥ���õ�һ��ɫ�����У�1��2��4��6��7��9��11��13��15��16��
��45�����˹���һֱȾ��ȥ���õ�һ��ɫ�����У�1��2��4��6��7��9��11��13��15��16��![]() �����������ɫ�������У���1��ʼ�ĵ�1000������_________
�����������ɫ�������У���1��ʼ�ĵ�1000������_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������![]() ��ͬѧ���С������ֱ�����Ϸ�������ǣ�
��ͬѧ���С������ֱ�����Ϸ�������ǣ�![]() ��ͬʱ���ѡ�����Ļ��ֱ�����һ�����ƣ��涨��ͬ��������������ÿ�˵�
��ͬʱ���ѡ�����Ļ��ֱ�����һ�����ƣ��涨��ͬ��������������ÿ�˵�![]() �֣�����ÿ�˵�
�֣�����ÿ�˵�![]() ��.��
��.��![]() �˹�������
�˹�������![]() ����Ϸ����С��
����Ϸ����С��![]() ����Ϸ�÷�֮��Ϊ
����Ϸ�÷�֮��Ϊ![]() ����
����![]() �� ��
�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com