
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与
与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,求直线
,求直线![]() 将
将![]() 分成的两部分的面积比.
分成的两部分的面积比.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
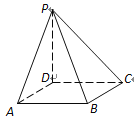
【题目】在四棱锥P–ABCD中,底面ABCD是边长为6的正方形,PD平面ABCD,PD=8.
(1) 求PB与平面ABCD所成角的大小;
(2) 求异面直线PB与DC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 | 途中速度( | 途中费用(元/ | 装卸时间( | 装卸费用(元/ |
汽车 | 50 | 80 | 2 | 200 |
火车 | 100 | 40 | 3 | 400 |
飞机 | 200 | 200 | 3 | 800 |
若这批海产品在运输过程中的损耗为300元/![]() ,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,两焦点与短轴的一个顶点构成等腰直角三角形,且点
,两焦点与短轴的一个顶点构成等腰直角三角形,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图所示,过椭圆的左焦点作直线![]() (斜率存在且不为0)交椭圆
(斜率存在且不为0)交椭圆![]() 于
于![]() 两点,过右焦点作直线
两点,过右焦点作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,动点
,动点![]() (异于
(异于![]() )在椭圆上运动.
)在椭圆上运动.
①证明: ![]() 为常数;
为常数;
②当![]() 时,利用上述结论求
时,利用上述结论求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每轮游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每轮游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓是否出现音乐相互独立.
,且各次击鼓是否出现音乐相互独立.
(1)玩三轮游戏,至少有一轮出现音乐的概率是多少?
(2)设每轮游戏获得的分数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
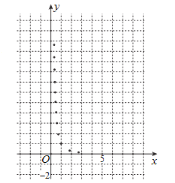
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关
关![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为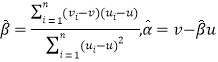 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() .如果数列
.如果数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“陪伴数列”.
的“陪伴数列”.
(Ⅰ)写出数列![]() 的“陪伴数列”
的“陪伴数列”![]() ;
;
(Ⅱ)若![]() 的“陪伴数列”是
的“陪伴数列”是![]() .试证明:
.试证明: ![]() 成等差数列.
成等差数列.
(Ⅲ)若![]() 为偶数,且
为偶数,且![]() 的“陪伴数列”是
的“陪伴数列”是![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com