
【题目】某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 | 途中速度( | 途中费用(元/ | 装卸时间( | 装卸费用(元/ |
汽车 | 50 | 80 | 2 | 200 |
火车 | 100 | 40 | 3 | 400 |
飞机 | 200 | 200 | 3 | 800 |
若这批海产品在运输过程中的损耗为300元/![]() ,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
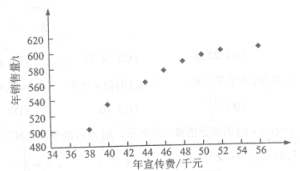
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]()
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前几年随着网购的普及,线下零售遭遇挑战,但随着新零售模式的不断出现,零售行业近几年呈现增长趋势,下表为![]() 年中国百货零售业销售额(单位:亿元,数据经过处理,
年中国百货零售业销售额(单位:亿元,数据经过处理, ![]() 分别对应
分别对应![]() ):
):
年份代码 | 1 | 2 | 3 | 4 |
销售额 | 95 | 165 | 230 | 310 |
(1)由上表数据可知,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,并预测2018年我国百货零售业销售额;
的回归方程,并预测2018年我国百货零售业销售额;
(3)从![]() 年这4年的百货零售业销售额及2018年预测销售额这5个数据中任取2个数据,求这2个数据之差的绝对值大于200亿元的概率.
年这4年的百货零售业销售额及2018年预测销售额这5个数据中任取2个数据,求这2个数据之差的绝对值大于200亿元的概率.
参考数据:
![]() ,
, 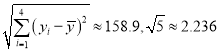
参考公式:相关系数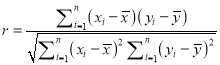 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为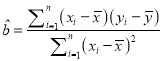 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
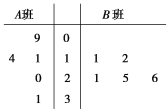
【题目】某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1) 试估计哪个班级学生平均上网的时间较长。
(2)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax-a),其中a是常数.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若存在实数k,使得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: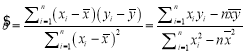 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与
与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,求直线
,求直线![]() 将
将![]() 分成的两部分的面积比.
分成的两部分的面积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com