
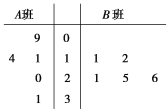
【题目】某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1) 试估计哪个班级学生平均上网的时间较长。
(2)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
【答案】(1)B班;(2)![]()
【解析】
(1)直接计算两班的上网时间的平均值,再比较即得解;(2)直接利用古典概型的概率公式求解.
(1)A班样本数据的平均值为![]() (9+11+14+20+31)=17.
(9+11+14+20+31)=17.
由此估计A班学生每周平均上网时间为17小时;
B班样本数据的平均值为![]() (11+12+21+25+26)=19,
(11+12+21+25+26)=19,
由此估计B班学生每周平均上网时间较长.
(2)A班的样本数据中不超过19的数据a有3个,分别为9,11,14,
B班的样本数据中不超过21的数据b也有3个,分别为11,12,21,
从A班和B班的样本数据中各随机抽取一个共有9种不同情况,
分别为(9,11),(9,12),(9,21),(11,11),(11,12),(11,21),(14,11),(14,12),(14,21),
其中a>b的情况有(14,11),(14,12)两种,
故a>b的概率p=![]() .
.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】甲乙两名运动员互不影响地进行四次设计训练,根据以往的数据统计,他们设计成绩均不低于8环(成绩环数以整数计),且甲乙射击成绩(环数)的分布列如下:
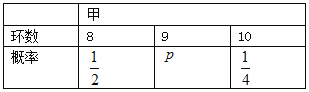
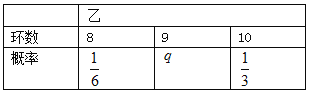
(I)求![]() ,
, ![]() 的值;
的值;
(II)若甲乙两射手各射击两次,求四次射击中恰有三次命中9环的概率;
(III)若两个射手各射击1次,记两人所得环数的差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市自来水公司对全市用户采用分段计费的方式计算水费,收费标准如下:不超过![]() 的部分为2.20元/
的部分为2.20元/![]() ;超过
;超过![]() 不超过
不超过![]() 的部分为2.80元/
的部分为2.80元/![]() ;超过
;超过![]() 部分为3.20元/
部分为3.20元/![]() .
.
(1)试求居民月水费y(元)关于用水量![]() 的函数关系式;
的函数关系式;
(2)某户居民4月份用水![]() ,应交水费多少元?
,应交水费多少元?
(3)若有一户居民5月份水费为57.20元,请问该户居民5月份用水多少?
(4)若某户居民6月份、7月份共用水![]() ,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 | 途中速度( | 途中费用(元/ | 装卸时间( | 装卸费用(元/ |
汽车 | 50 | 80 | 2 | 200 |
火车 | 100 | 40 | 3 | 400 |
飞机 | 200 | 200 | 3 | 800 |
若这批海产品在运输过程中的损耗为300元/![]() ,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com