
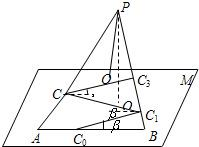
 某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2Km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2Km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=| 2 |
| 5 |
| 1 |
| 4 |
| x2+100 |
| 2 |
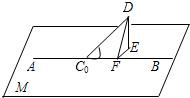 解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,
解(1)在盘山公路C0C1上任选一点D,作DE⊥平面M交平面M于E,过E作EF⊥AB交AB于F,| 2 |
| 5 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 10 |
| 5 |
| 2 |
| 5 |
| 2 |
| (10x)2+100 |
| 5 |
| 2 |
| 2 |
| x2+1 |
| 2 |
| 2 |
| 10x | ||
|
| 2 |


科目:高中数学 来源: 题型:
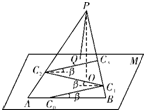 (2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
(2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=| 2 |
| 5 |
| 1 |
| 4 |
| x2+100 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市高三第六次月考理科数学卷 题型:解答题
(本小题满分13分)
某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=.现从山脚的水平公路AB某处C0开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为C0C1,C1C2,C2C3,…,Cn-1Cn(如图所示),且C0C1,C1C2,C2C3,…,Cn-1Cn与AB所成的角均为β,其中0<β<90°,sinβ=.试问:
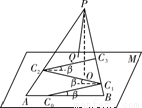
(1)每修建盘山公路多少米,垂直高度就能升高100米.若修建盘山公路至半山腰(高度为山高的一半),在半山腰的中心Q处修建上山缆车索道站,索道PQ依山而建(与山坡面平行,离坡面高度忽略不计),问盘山公路的长度和索道的长度各是多少?
(2)若修建xkm盘山公路,其造价为 a万元.修建索道的造价为2a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省长沙一中高三(下)第六次月考数学试卷(理科)(解析版) 题型:解答题
 .现从山脚的公路AB某处C开始修建与公路AB成β角的盘山公路CC1,C1C2,C2C3,…Cn-1Cn(如图所示).其中0<β<90°,sinβ=
.现从山脚的公路AB某处C开始修建与公路AB成β角的盘山公路CC1,C1C2,C2C3,…Cn-1Cn(如图所示).其中0<β<90°,sinβ=
 万元.而修建索道的造价为2
万元.而修建索道的造价为2 a元/Km.
a元/Km.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省永州市蓝山二中高三第六次联考数学试卷(理科)(解析版) 题型:解答题
 .现从山脚的水平公路AB某处C开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为
.现从山脚的水平公路AB某处C开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为 .试问:
.试问: a万元.修建索道的造价为2
a万元.修建索道的造价为2 a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com