
【题目】已知函数 ![]() .
.
(1)求函数f(x)的单调区间;
(2)证明:若a<5,则对任意 ![]() ,有
,有 ![]() .
.
【答案】
(1)解:f(x)的定义域为(0,+∞),
![]() ,
,
∵a﹣1≥1
当a﹣1>1时,即a>2时,f(x)的单调增区间为(0,1),(a﹣1,+∞);
单调减区间为(1,a﹣1).
当a﹣1=1时,即a=2时,f(x)的单调增区间为(0,+∞)
(2)要证:对任意 ![]() ,
,
有 ![]() .
.
不防设x1>x2,
即证f(x1)﹣f(x2)>﹣(x1﹣x2)
即证f(x1)+x1>f(x2)+x2
设 ![]() ,x>0
,x>0
即证当x1>x2时,g(x1)>g(x2).
即证g(x)在(0,+∞)单调递增.
∵ ![]()
而△=(a﹣1)2﹣4(a﹣1)=(a﹣1)(a﹣5)
又∵2≤a<5,
∴△<0,
∴x2﹣(a﹣1)x+(a﹣1)>0恒成立,
∴ ![]() 对x∈(0,+∞)恒成立,
对x∈(0,+∞)恒成立,
∴g(x)在(0,+∞)单调递增.
∴原题得证.
【解析】(1)由 ![]() ,得当a﹣1>1时,即a>2时,f(x)的单调增区间为(0,1),(a﹣1,+∞);单调减区间为(1,a﹣1).当a﹣1=1时,即a=2时,f(x)的单调增区间为(0,+∞)(2)要证:对任意
,得当a﹣1>1时,即a>2时,f(x)的单调增区间为(0,1),(a﹣1,+∞);单调减区间为(1,a﹣1).当a﹣1=1时,即a=2时,f(x)的单调增区间为(0,+∞)(2)要证:对任意 ![]() ,有
,有 ![]() .即证f(x1)+x1>f(x2)+x2设
.即证f(x1)+x1>f(x2)+x2设 ![]() ,x>0,即证g(x)在(0,+∞)单调递增.由
,x>0,即证g(x)在(0,+∞)单调递增.由 ![]() ,由g(x)在(0,+∞)单调递增,从而原题得证.
,由g(x)在(0,+∞)单调递增,从而原题得证.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①f(x)=x3﹣3x2是增函数,无极值.
②f(x)=x3﹣3x2在(﹣∞,2)上没有最大值
③由曲线y=x,y=x2所围成图形的面积是 ![]()
④函数f(x)=lnx+ax存在与直线2x﹣y=0平行的切线,则实数a的取值范围是(﹣∞,2)
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数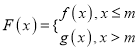 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组: ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
(1)求该社区参加健美操运动人员的平均年龄;
(2)如果研究小组从该样本中年龄在![]() 和
和![]() 的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在
的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为( )
A.(0,+∞)
B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(0,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
x | 3 | ﹣2 | 4 |
|
y | ﹣2 | 0 | ﹣4 |
|
(1)求C1、C2的标准方程;
(2)请问是否存在直线l满足条件:①过C2的焦点F;②与C1交不同两点M、N且满足 ![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com