
【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数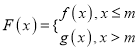 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
【答案】(1)[0, ![]() ].(2)e-1≤a≤e2-e.
].(2)e-1≤a≤e2-e.
【解析】试题分析:(1)①由![]() ,得到函数
,得到函数![]() ,求得
,求得![]() ,利用
,利用![]() ,
, ![]() ,即可求解函数的单调区间;②由
,即可求解函数的单调区间;②由![]() ,得出函数
,得出函数![]() 的单调区间,分
的单调区间,分![]() 和
和![]() 分离讨论,即可求解实数
分离讨论,即可求解实数![]() 的取值范围;
的取值范围;
(2)由![]() ,若
,若![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,不符合题意,
单调递增,不符合题意,
当![]() 时,得出
时,得出![]() 的单调性,不妨设
的单调性,不妨设![]() 时,有
时,有![]() ,利用函数的单调性得到
,利用函数的单调性得到![]() ,列出不等式组,即可求解
,列出不等式组,即可求解![]() 范围。
范围。
试题解析:
(1)当a=e时,f (x)=ex-ex-1.
① h (x)=f (x)-g (x)=ex-2x-1,h′ (x)=ex-2.
由h′ (x)>0得x>ln2,由h′ (x)<0得x<ln2.
所以函数h(x)的单调增区间为 (ln2,+∞),单调减区间为 (-∞,ln2).
② f ′ (x)=ex-e.
当x<1时,f′ (x)<0,所以f (x)在区间(-∞,1)上单调递减;
当x>1时,f′ (x)>0,所以f(x)在区间(1,+∞)上单调递增.
1° 当m≤1时,f (x)在(-∞,m]上单调递减,值域为[em-em-1,+∞),
g(x)=(2-e)x在(m,+∞)上单调递减,值域为(-∞,(2-e)m),
因为F(x)的值域为R,所以em-em-1≤(2-e)m,
即em-2m-1≤0. (*)
由①可知当m<0时,h(m)=em-2m-1>h(0)=0,故(*)不成立.
因为h(m)在(0,ln2)上单调递减,在(ln2,1)上单调递增,且h(0)=0,h(1)=e-3<0,
所以当0≤m≤1时,h(m)≤0恒成立,因此0≤m≤1.
2° 当m>1时,f (x)在(-∞,1)上单调递减,在(1,m]上单调递增,
所以函数f (x)=ex-ex-1在(-∞,m]上的值域为[f (1),+∞),即[-1,+∞).
g(x)=(2-e)x在(m,+∞)上单调递减,值域为(-∞,(2-e)m).
因为F(x)的值域为R,所以-1≤(2-e)m,即1<m≤![]() .
.
综合1°,2°可知,实数m的取值范围是[0,![]() ].
].
(2)f ′ (x)=ex-a.
若a≤0时,f ′ (x)>0,此时f(x)在R上单调递增.
由f(x1)=f(x2)可得x1=x2,与|x1-x2|≥1相矛盾,
所以a>0,且f(x)在(-∞,lna]单调递减,在[lna,+∞)上单调递增.
若x1,x2∈(-∞,lna],则由f (x1)=f (x2)可得x1=x2,与|x1-x2|≥1相矛盾,
同样不能有x1,x2∈[lna,+∞).
不妨设0≤x1<x2≤2,则有0≤x1<lna<x2≤2.
因为f(x)在(x1,lna)上单调递减,在(lna,x2)上单调递增,且f (x1)=f (x2),
所以当x1≤x≤x2时,f (x)≤f (x1)=f (x2).
由0≤x1<x2≤2,且|x1-x2|≥1,可得1∈[x1,x2],
故f (1)≤f (x1)=f (x2).
又f (x)在(-∞,lna]单调递减,且0≤x1<lna,所以f (x1)≤f (0),
所以f (1)≤f (0),同理f (1)≤f (2).
即![]() 解得e-1≤a≤e2-e-1,
解得e-1≤a≤e2-e-1,
所以 e-1≤a≤e2-e.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:
【题目】本公司计划2008年在甲,乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲,乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲,乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲,乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( ) 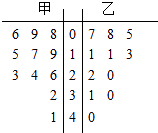
A.19、13
B.13、19
C.20、18
D.18、20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查,得到如下的列联表.
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为 ![]() ,
,
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3名进行其它方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布列、数学期望以及方差.
下面的临界值表仅供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角△ABC,AB=AC=3,P,Q分别为边AB,BC上的点,M,N是平面上两点,若 ![]() +
+ ![]() =0,(
=0,( ![]() +
+ ![]() )
) ![]() =0,
=0, ![]() =3
=3 ![]() ,且直线MN经过△ABC的外心,则
,且直线MN经过△ABC的外心,则 ![]() =( )
=( )
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com