
【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( ) 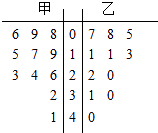
A.19、13
B.13、19
C.20、18
D.18、20
【答案】A
【解析】解:由茎叶图知甲的分数是6,8,9,15,17,19,23,24,26,32,41,
共有11个数据,中位数是最中间一个19,
乙的数据是5,7,8,11,11,13,20,22,30,31,40
共有11和数据,中位数是最中间一个13,
故选A.
【考点精析】本题主要考查了茎叶图和平均数、中位数、众数的相关知识点,需要掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据才能正确解答此题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,x∈(﹣2,2)
,x∈(﹣2,2)
(1)判断f(x)的奇偶性并说明理由;
(2)求证:函数f(x)在(﹣2,2)上是增函数;
(3)若f(2+a)+f(1﹣2a)>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为实数集R,A={x|3≤x<7},B={x| ![]() ≤2x≤8},C={x|x<a}.
≤2x≤8},C={x|x<a}.
(1)求R(A∪B)
(2)如果A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数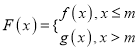 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组: ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
(1)求该社区参加健美操运动人员的平均年龄;
(2)如果研究小组从该样本中年龄在![]() 和
和![]() 的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在
的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益函数为R(x)= 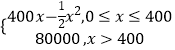 ,其中x是仪器的产量(单位:台);
,其中x是仪器的产量(单位:台);
(1)将利润f(x)表示为产量x的函数(利润=总收益﹣总成本);
(2)当产量x为多少台时,公司所获利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com