
【题目】已知f(x)= ![]() ,x∈(﹣2,2)
,x∈(﹣2,2)
(1)判断f(x)的奇偶性并说明理由;
(2)求证:函数f(x)在(﹣2,2)上是增函数;
(3)若f(2+a)+f(1﹣2a)>0,求实数a的取值范围.
【答案】
(1)解:函数f(x)= ![]() 是定义域(﹣2,2)上的奇函数,
是定义域(﹣2,2)上的奇函数,
理由如下,
任取x∈(﹣2,2),有f(﹣x)= ![]() =﹣
=﹣ ![]() =﹣f(x),
=﹣f(x),
所以f(x)是定义域(﹣2,2)上的奇函数
(2)证明:设x1,x2为区间(﹣2,2)上的任意两个值,
且x1<x2,则
![]() =
= ![]() ;
;
因为﹣2<x1<x2<2,
所以 x2﹣x1>0,x1x2﹣4<0,
即f(x1)﹣f(x2)<0;
所以函数f(x)在(﹣2,2)上是增函数
(3)解:因为f(x)为奇函数,
所以由f(2+a)+f(1﹣2a)>0,
得f(2+a)>﹣f(1﹣2a)=f(2a﹣1),
又因为函数f(x)在(﹣2,2)上是增函数,
所以  ;
;
解得  ,
,
即实数a的取值范围是(﹣ ![]() ,0)
,0)
【解析】(1)利用奇偶性的定义判断函数f(x)是定义域上的奇函数;(2)根据单调性的定义证明f(x)是(﹣2,2)上的增函数;(3)根据f(x)为奇函数且在(﹣2,2)上是增函数,转化不等式f(2+a)+f(1﹣2a)>0,求出a的取值范围.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数的奇偶性的理解,了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+b+1(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)= ![]() .
.
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题中:
①设有一个回归方程 ![]() =2﹣3x,变量x增加一个单位时,y平均增加3个单位;
=2﹣3x,变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)对任意x∈R都有f(x)=f(x+4),当x∈(﹣2,0)时,f(x)=2x , 则f(2016)﹣f(2015)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)证明f(x)为偶函数;
(2)若不等式k≤xf(x)+ ![]() 在x∈[1,3]上恒成立,求实数k的取值范围;
在x∈[1,3]上恒成立,求实数k的取值范围;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( ) 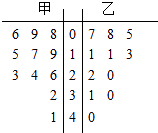
A.19、13
B.13、19
C.20、18
D.18、20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com