Question

已知是椭圆的左、右焦点，是椭圆上位于第一象限内的一点，点也在椭圆上，且满足（是坐标原点），，若椭圆的离心率为.

（1）若的面积等于，求椭圆的方程；

（2）设直线与（1）中的椭圆相交于不同的两点，已知点的坐标为（），点在线段的垂直平分线上，且，求的值.

 

Answer 1

【答案】

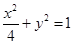（1）   （2）

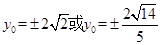
【解析】

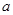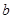试题分析：（1）利用离心率沟通和及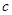的关系，再由三角形面积得到另一个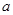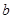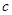，，的关系，

可求得椭圆方程为：．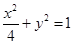

（3）由（2）可知A（-2,0）．设B点的坐标为（x_1,,y₁）,直线l的斜率为k，则直线l的方程为y=k(x+2),

于是A,B两点的坐标满足方程组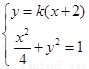

由方程组消去y并整理，得

由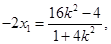得

设线段AB是中点为M，则M的坐标为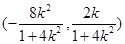

以下分两种情况：

①当k=0时，点B的坐标为（2,0）．线段AB的垂直平分线为y轴，于是

．

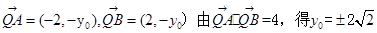②当K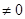时，线段AB的垂直平分线方程为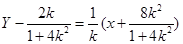

令x=0，解得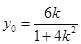

由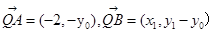

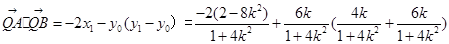
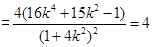
整理得．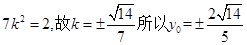

经验证，都符合题意，故．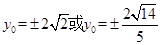

考点：线与圆锥曲线的关系；椭圆的标准方程；椭圆的简单性质．

点评：本题考查了椭圆的标准方程，考查了椭圆的简单几何性质，主要考查了直线与圆锥曲线的综合问题．解题的过程一般是把直线与圆锥曲线的方程联立，利用韦达定理和判别式来作为解题的关键．