
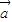 、
、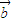 、
、 、
、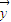 四个向量,满足
四个向量,满足 =
=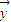 -
-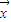 ,
, =2
=2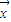 -
- ,
, ⊥
⊥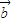 ,|
,|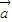 |=|
|=|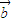 |=1,设θ为
|=1,设θ为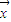 ,
,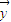 的夹角,则cosθ= .
的夹角,则cosθ= . 科目:高中数学 来源: 题型:
| a |
| a |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
①已知x、y为实数,则x2≠y2![]() x≠y且x≠-y;
x≠y且x≠-y;
②如果P、q都是r的必要条件,s是r的充分条件,q是s的充分条件,则P是q的充分但不必要条件;
③设平面内有△ABC,且P表示平面内的点,则{P|PA=PB}∩{P|PA=PC}={P是△ABC的垂心};
④如果用P,q分别表示原命题“梯形的四条边不全相等”的条件和结论,那么该原命题的“若![]() q,则
q,则![]() P”的形式的命题为:“四条边完全相等的四边形不是梯形”.上述命题中正确命题的序号为
P”的形式的命题为:“四条边完全相等的四边形不是梯形”.上述命题中正确命题的序号为
A.①③ B.②④ C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源:广东省09-10学年高一下学期期末考试数学试题 题型:解答题
(本小题满分14分)
设平面内有四个向量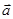 、
、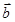 、
、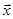 、
、 ,且满足
,且满足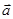 =
= -
-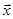 ,
,
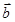 =2
=2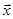 -
- ,
,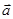 ⊥
⊥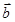 , |
, |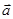 |=|
|=|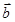 |=1.
|=1.
(1)求|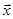 |,|
|,| |;
|;
(2)若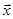 、
、 的夹角为
的夹角为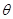 ,求cos
,求cos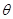 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com