
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 上涨率y | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
分析 (1)利用已知条件求出回归直线方程的有关数据,即可求出回归直线方程.
(2)代入回归直线方程,即可预测该地6月份上涨的百分率.
解答 解:(1)由题意,$\overline{x}$=3,$\overline{y}$=0.2…(2分)
12+22+32+42+52=55,…(3分)
1×0.1+2×0.2+3×0.3+4×0.3+5×0.1=3.1…(4分)
所以$\hat b═\frac{{\sum_{i=1}^5{{x_i}{y_i}}-5\overline x•\overline y}}{{\sum_{i=1}^5{{x_i}^2-5{{\overline x}^2}}}}=\frac{3.1-5×3×0.2}{{55-5×{3^2}}}=0.01$…(6分)
$\hat a=\bar y-\hat b\overline{x}=0.2-0.01×3=0.17$…(7分)
∴回归直线方程为y=0.01x+0.17…(8分)
(2)当x=6时,y=0.01×6+0.17=0.23…(9分)
预测该地6月份上涨的百分率是0.23…(10分)
点评 本题考查回归直线方程的应用,回归直线方程的求法,考查计算能力.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a1a2>0,则a2a3>0 | B. | 若a1+a3<0,则a5<0 | ||
| C. | 若a1a2<0,则a1a5<0 | D. | 若0<a1<a2,则a1+a3>2a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0) | C. | (0,∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年利润 | 1.2万元 | 1.0万元 | 0.9万元 |
| 频数 | 20 | 60 | 40 |
| 合格次数 | 2次 | 1次 | 0次 |
| 年利润 | 1.3万元 | 1.1万元 | 0.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
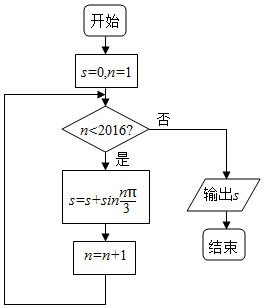 某程序框图如图所示,则该程序运行后输出的值是( )
某程序框图如图所示,则该程序运行后输出的值是( )| A. | 0 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | $504\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
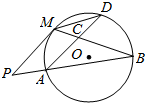 如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则CD等于( )
如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则CD等于( )| A. | $\frac{16}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{9}{16}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com