
【题目】已知函数f(x)=a( ![]() )x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
)x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
A.(0,4)
B.[0,4]
C.(0,4]
D.[0,4)
【答案】A
【解析】解:设x1∈{x|f(x)=0}={x|f(f(x))=0},
则f(x1)=0,且f(f(x1))=0,
∴f(0)=0,即a( ![]() )x=0
)x=0
∴a=0;
故f(x)=bx2+cx;
由f(x)=0得,x=0或x=﹣ ![]() ;
;
f(f(x))=b(bx2+cx)2+c(bx2+cx)=0,
整理得:(bx2+cx)(b2x2+bcx+c)=0,
当c=0时,显然成立;
当c≠0时,方程b2x2+bcx+c=0无根,
故△=(bc)2﹣4b2c<0,
解得,0<c<4.
综上所述,0≤c<4,
故答案选:A.
【考点精析】通过灵活运用函数的零点与方程根的关系,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,M,N,K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点. 
(1)求证:AN∥平面A1MK;
(2)求证:平面A1B1C⊥平面A1MK.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(x+ ![]() )的图象,只需把y=sinx图象上所有的点( )
)的图象,只需把y=sinx图象上所有的点( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<a<1,f(x)=ax , g(x)=logax,h(x)= ![]() ,当x>1时,则有( )
,当x>1时,则有( )
A.f(x)<g(x)<h(x)
B.g(x)<f(x)<h(x)
C.g(x)<h(x)<f(x)
D.h(x)<g(x)<f(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax+1﹣lnx.
(1)当a=3时,求函数f(x)的单调递增区间;
(2)若f(x)在区间(0, ![]() )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b∈R,函数f(x)=4ax2﹣2bx﹣a+b,x∈[0,1].
(1)当a=b=2时,求函数f(x)的最大值;
(2)证明:函数f(x)的最大值|2a﹣b|+a;
(3)证明:f(x)+|2a﹣b|+a≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了6个试销售数据,得到第i个销售单价xi(单位:元)与销售yi(单位:件)的数据资料,算得 ![]()
(1)求回归直线方程 ![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本) 附:回归直线方程 ![]() 中,
中, ![]() =
= 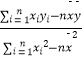 ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中
,其中 ![]() ,
, ![]() 是样本平均值.
是样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 通项公式为 ![]() .
.
(1)计算f(1),f(2),f(3)的值;
(2)比较f(n)与1的大小,并用数学归纳法证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com