
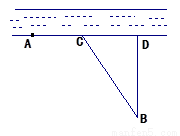
 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40 km的B处,乙厂到河岸的垂足D与A相距50 km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40 km的B处,乙厂到河岸的垂足D与A相距50 km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3![]() 元和5
元和5![]() 元,问供水站C建在岸边何处才能使水管费用最省?
元,问供水站C建在岸边何处才能使水管费用最省?
解法一:根据题意知,只有点C在线段AD上某一适当位置,才能使总运费最省,设C点距D点x km, 则 ∵BD=40,AC=50-![]() ,∴BC=
,∴BC=![]()
又设总的水管费用为y元,依题意有:![]() =3
=3![]() (50-x)+5
(50-x)+5![]()
![]()
![]()
y′=-3![]() +
+![]() ,令y′=0,解得
,令y′=0,解得![]() =30
=30
在(0,50)上,y只有一个极值点,根据实际问题的意义,
函数在![]() =30(km)处取得最小值,此时AC=50-
=30(km)处取得最小值,此时AC=50-![]() =20(km)
=20(km)
∴供水站建在A、D之间距甲厂20 km处,可使水管费用最省.
解法二:设∠BCD=![]() ,则BC=
,则BC=![]() ,CD=
,CD=![]() ,
, ![]()
设总的水管费用为f(θ),依题意,有
![]() (θ)=3
(θ)=3![]() (50-40?cotθ)+5
(50-40?cotθ)+5![]() =150
=150![]() +40
+40![]() ?
?![]()
∴![]() (θ)=40
(θ)=40![]()
![]()
令![]() (θ)=0,得cosθ=
(θ)=0,得cosθ=![]()
根据问题的实际意义,当cosθ=![]() 时,函数取得最小值,此时sinθ=
时,函数取得最小值,此时sinθ=![]() ,∴cotθ=
,∴cotθ=![]() ,
,
∴AC=50-40cotθ=20(km),即供水站建在A、D之间距甲厂20 km处,可使水管费用最省.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
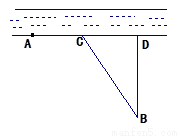
有甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
有甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省?

查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:解答题
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40 km的B处,乙厂到河岸的垂足D与A相距50 km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3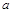 元和5
元和5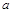 元,问供水站C建在岸边何处才能使水管费用最省?
元,问供水站C建在岸边何处才能使水管费用最省?
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高数选修1-1 3.4生活中的优化问题举例练习卷(解析版) 题型:解答题
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40 km的B处,乙厂到河岸的垂足D与A相距50 km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3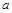 元和5
元和5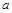 元,问供水站C建在岸边何处才能使水管费用最省?
元,问供水站C建在岸边何处才能使水管费用最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com