
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
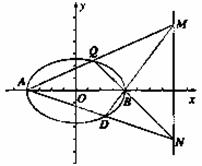
已知动点P到点A(-2,0)与点B(2,0)的斜率之积为-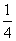 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M,N两点,直线BM与椭圆的交点为D.求证,A,D,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
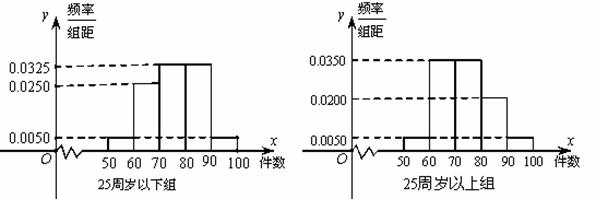
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2) 若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”; “25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数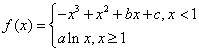 的图像过坐标原点
的图像过坐标原点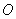 ,且在点
,且在点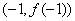 处的切线斜率为
处的切线斜率为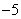 .
.
(1) 求实数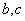 的值;
的值;
(2) 求函数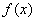 在区间
在区间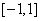 上的最小值;
上的最小值;
(3) 若函数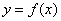 的图像上存在两点
的图像上存在两点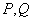 ,使得对于任意给定的正实数
,使得对于任意给定的正实数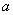 都满足
都满足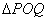 是以
是以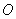 为直角顶点的直角三角形,且三角形斜边中点在
为直角顶点的直角三角形,且三角形斜边中点在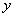 轴上,求点
轴上,求点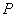 的横坐标的取值范围.
的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
等边三角形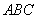 的边长为3,点
的边长为3,点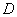 、
、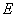 分别是边
分别是边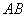 、
、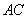 上的点,且满足
上的点,且满足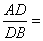
 (如图4).将△
(如图4).将△ 沿
沿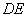 折起到△
折起到△ 的位置,使二面角
的位置,使二面角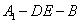 成直二面角,连结
成直二面角,连结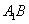 、
、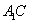
(如图5).
(1)求证: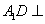 平面
平面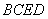 ;
;
(2)在线段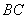 上是否存在点
上是否存在点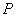 ,使直线
,使直线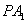 与平面
与平面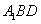 所成的角为
所成的角为 ?若存在,求出
?若存在,求出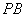 的长,若不存在,请说明理由
的长,若不存在,请说明理由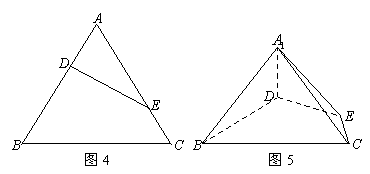 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com