
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证:![]() 为定值;
为定值;
(3)当![]() 取得最大值时,求
取得最大值时,求![]() .
.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)首先根据条件设出圆心及半径,然后利用弦长公式求得半径,再利用点到直线的距离公式求得圆心,从而求得圆![]() 的方程;(2)直线
的方程;(2)直线![]() 的斜率不存在可直接求出定值,直线
的斜率不存在可直接求出定值,直线![]() 与直线
与直线![]() 的斜率存在时,设点
的斜率存在时,设点![]() ,由此得到直线
,由此得到直线![]() 的方程与
的方程与![]() 的方程,从而求得点
的方程,从而求得点![]() 的坐标,进而利用向量数量积公式求出定值;(3)首先求得
的坐标,进而利用向量数量积公式求出定值;(3)首先求得![]() 关于
关于![]() 的表达式,然后根据直线
的表达式,然后根据直线![]() 与圆位置关系求得
与圆位置关系求得![]() 的值.
的值.
试题解析:(1) 易知点![]() 在线段
在线段![]() 的中垂线
的中垂线![]() 上,故可设
上,故可设![]() ,圆
,圆![]() 的半径为
的半径为![]()
∵直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() ,且
,且![]()
∴![]() 到直线
到直线![]() 的距离
的距离![]() ,或
,或![]() .
.
又圆![]() 的圆心在圆
的圆心在圆![]() 的内部,
的内部,
![]() ,圆
,圆![]() 的方程
的方程![]() .
.
(2)证明: 当直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 与直线
与直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
令![]() 得
得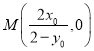 .直线
.直线![]() 的方程为
的方程为![]() .
.
令![]() 得
得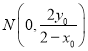 .
.
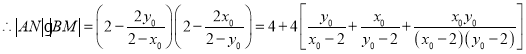
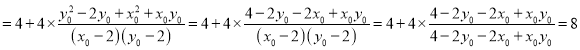 ,
,
故![]() 为定值为
为定值为![]() .
.
(3)解: ![]()
设![]() ,易知当直线
,易知当直线![]() 与圆
与圆![]() 切于第三象限时,
切于第三象限时,![]() 取得最小值,
取得最小值,
此时![]() , 此时,
, 此时,![]() ,故
,故![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租.该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东![]() 且与点A相距40
且与点A相距40![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() +
+![]() (其中sin
(其中sin![]() =
=![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式:  ,
, ![]() =
=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求△
,求△![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是枣强县普通职工
是枣强县普通职工![]() (
(![]() ,
,![]() )个人的年收入,设
)个人的年收入,设![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增加,中位数一定变大,方差可能不变
B.年收入平均数大大增加,中位数可能不变,方差变大
C.年收入平均数大大增加,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com