
已知函数 .
.
(Ⅰ) 求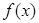 的单调区间;
的单调区间;
(Ⅱ) 求所有的实数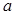 ,使得不等式
,使得不等式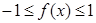 对
对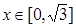 恒成立.
恒成立.
(Ⅰ)当a≤0时, f(x)的增区间是(-∞,+∞);当a>0时,f(x)的增区间是(-∞,-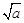 ]、[
]、[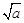 ,+∞),f(x)的减区间是[-
,+∞),f(x)的减区间是[-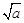 ,
,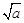 ];(Ⅱ)
];(Ⅱ)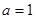
解析试题分析:(Ⅰ)本小题首先求函数的导数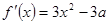 ,利用导数的正负求解原函数的单调区间,注意参数
,利用导数的正负求解原函数的单调区间,注意参数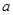 的范围,通过分情况讨论可以分别得出函数
的范围,通过分情况讨论可以分别得出函数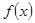 的增减区间;(Ⅱ)根据第一问可知函数
的增减区间;(Ⅱ)根据第一问可知函数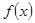 在区间
在区间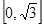 上的单调性,进而可以求得函数
上的单调性,进而可以求得函数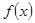 在区间
在区间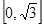 上的的最大值和最小值,然后让
上的的最大值和最小值,然后让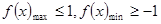 ,即可解得参数
,即可解得参数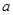 的取值范围.
的取值范围.
试题解析:(Ⅰ) f′(x)=3x2-3a.
当a≤0时,f′(x)≥0恒成立,故f(x)的增区间是(-∞,+∞).
当a>0时,由f′(x)>0,得 x<-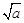 或 x>
或 x>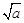 ,
,
故f(x)的增区间是(-∞,-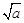 ]和[
]和[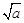 ,+∞),f(x)的减区间是[-
,+∞),f(x)的减区间是[-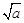 ,
,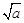 ]. 7分
]. 7分
(Ⅱ) 当a≤0时,由(Ⅰ)知f(x)在[0,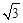 ]上递增,且f(0)=1,此时无解.
]上递增,且f(0)=1,此时无解.
当0<a<3时,由(Ⅰ)知f(x)在[0,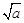 ]上递减,在[
]上递减,在[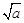 ,
,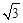 ]上递增,
]上递增,
所以f(x)在[0,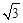 ]上的最小值为f(
]上的最小值为f(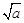 )=1-2a
)=1-2a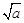 .
.
所以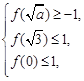
即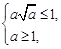
所以a=1.
当a≥3时,由(Ⅰ)知f(x)在[0,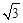 ]上递减,又f(0)=1,所以
]上递减,又f(0)=1,所以
f(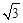 )=3
)=3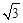 -3
-3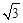 a+1≥-1,
a+1≥-1,
解得a≤1+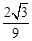 ,此时无解.
,此时无解.
综上,所求的实数a=1. 15分
考点:1.导数判断单调性;2.解不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 .
.
(1)当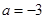 ,
,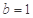 时,求函数
时,求函数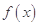 的最大值;
的最大值;
(2)令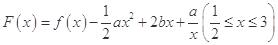 ,其图象上存在一点
,其图象上存在一点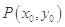 ,使此处切线的斜率
,使此处切线的斜率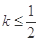 ,求实数
,求实数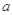 的取值范围;
的取值范围;
(3)当 ,
,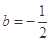 时,方程
时,方程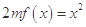 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com