练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

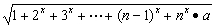    设函数f（x）=Equation.3其中a∈R，n是任意给定的自然数，n≥2，如果在x∈（-∞，1］上有意义，求a的取值范围.

    解：依题意，1+2x+3x+…+（n-1）x+nxa≥0（x≤1）恒成立，即a≥（x≤1）恒成立.

     

    设g（x）=-[，因-（）x（m=1，2，…，n-1）在（-∞，1]上均为增函数，故g（x）在（-∞，1]上为增函数.从而，g（x）≤g（1）=-（所以，当a≥时，a≥g（x）在（-∞，1）上恒成立.

    因此，a的取值范围是［，+∞）.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012-2013学年浙江省嘉兴市高三（上）基础测试数学试卷（理科）（解析版） 题型：选择题

    设函数f（x）=其中[x]表示不超过x的最大整数，如[-1.3]=-2，[1.3]=1，则函数y=f（x）-x-不同零点的个数（ ）
    A．2
    B．3
    C．4
    D．5

    查看答案和解析>>

    科目：高中数学 来源：2013年安徽省池州市东至县高考数学一模试卷（文科）（解析版） 题型：解答题

    设函数f（x）=•其中向量=（2cosx，1），．
    （1）求函数f（x）的最小正周期和在[0，π]上的单调递增区间；
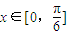    （2）当时，f（x）的最大值为4，求m的值．

    查看答案和解析>>

    科目：高中数学 来源：3年高考2年模拟：4.2 三角函数的图象和性质及三角恒等变换（6）（解析版） 题型：解答题

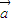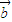    设函数f（x）=•其中向量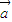=（2cosx，1），．
    （1）求函数f（x）的最小正周期和在[0，π]上的单调递增区间；
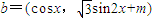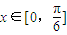    （2）当时，f（x）的最大值为4，求m的值．

    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省重点高中协作体高考夺标预测数学试卷（2）（解析版） 题型：解答题

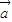    设函数f（x）=•其中向量=（2cosx，1），．
    （1）求函数f（x）的最小正周期和在[0，π]上的单调递增区间；
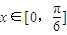    （2）当时，f（x）的最大值为4，求m的值．

    查看答案和解析>>

    同步练习册答案