
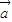 •
• 其中向量
其中向量 =(2cosx,1),
=(2cosx,1), .
.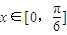 时,f(x)的最大值为4,求m的值.
时,f(x)的最大值为4,求m的值.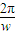 可求得最小正周期,再由正弦函数的单调性可求得单调递增区间.
可求得最小正周期,再由正弦函数的单调性可求得单调递增区间. 时函数f(x)单调递增,进而可得到当
时函数f(x)单调递增,进而可得到当 时f(x)取最大值,然后将
时f(x)取最大值,然后将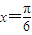 代入即可求得m的值.
代入即可求得m的值. ,
, .
. .
.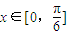 时,
时, 时,f(x)取最大值为m+3,即m+3=4.解得m=1,
时,f(x)取最大值为m+3,即m+3=4.解得m=1,

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 4 |
| x+1 |
| x2+x |
| 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2+…+xn |
| n |
| f(x1)+f(x2)+…+f(xn) |
| n |
| AC |
| CB |
| x1+λx2 |
| 1+λ |
| f(x1)+λf(x2) |
| 1+λ |
3
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| AC |
| CB |
| x1+λx2 |
| 1+λ |
| f(x1)+λf(x2) |
| 1+λ |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市高二(上)期末数学试卷(文科)(解析版) 题型:填空题
 x3-x2+x+1;
x3-x2+x+1; ;
; ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com