
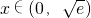 递减;
递减; ;
;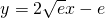 .
.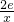 ,x>0.由f′(x)=2x-
,x>0.由f′(x)=2x-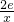 =0,x>0,得x=
=0,x>0,得x= ,列表讨论,能求出f(x)=h(x)-m(x)在
,列表讨论,能求出f(x)=h(x)-m(x)在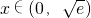 递减;
递减;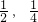 ),把(
),把(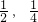 )代入y=x+b,得b=-
)代入y=x+b,得b=- ,故h(x)和φ(x)存在“隔离直线”y=kx+b,且b的最大值为
,故h(x)和φ(x)存在“隔离直线”y=kx+b,且b的最大值为 ;
;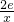 ,x>0.由f′(x)=2x-
,x>0.由f′(x)=2x-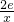 =0,x>0,得x=
=0,x>0,得x= ,
, )
)  (
(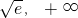 ) f′(x)- 0+ f(x)↓ 极小值↑∴f(x)=h(x)-m(x)在
) f′(x)- 0+ f(x)↓ 极小值↑∴f(x)=h(x)-m(x)在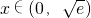 递减,故①正确;
递减,故①正确;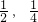 ),
),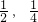 )代入y=x+b,得b=-
)代入y=x+b,得b=- ,
, ,故③正确;
,故③正确;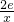 =0,x>0,得x=
=0,x>0,得x= ,
, 处有公共点.
处有公共点. ),即y=kx-k
),即y=kx-k +e.
+e. +e可得 x2-kx+k
+e可得 x2-kx+k -e≥0当x∈R恒成立,
-e≥0当x∈R恒成立, +4e=(k-2
+4e=(k-2 )2≤0,只有k=2
)2≤0,只有k=2 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2 x-e.
x-e. +e,可得只有k=2
+e,可得只有k=2 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2 x-e.
x-e. x-e,故④正确.
x-e,故④正确.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| e |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| e |
| 1 |
| 4 |
| e |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省广州市执信中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三12月练习数学试卷 题型:填空题
若存在实常数k和b,使函数 和
和 对其定义域上的任意实数x恒有:
对其定义域上的任意实数x恒有:
 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”。
的“隔离直线”。
已知 ,则可推知
,则可推知 的“隔离直线”方程为 ▲
的“隔离直线”方程为 ▲
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com