
分析 (1)求出g(x)的解析式以及a的值,从而求出g(f(x))的解析式,求出函数 的单调区间即可;
(2)令φ(x)=f(x)h(x)-$\frac{1}{x}$,(x>0),根据函数的单调性得到φ(x)在(0,+∞)递增;从而证出结论.
解答 解:(1)函数g(x)是h(x)=ex的反函数,
可得g(x)=lnx;
函数f(x)=x2+ax(a>0)在[-1,2]上的最大值为8,
只能是f(-1)=8或f(2)=8,
即有1-a=8或4+2a=8,
解得a=2(-7舍去),
函数g(f(x))=ln(x2+2x),
由x2+2x>0,可得x>0或x<-2.
由复合函数的单调性,可得
函数g(f(x))的单调增区间为(0,+∞);
单调减区间为(-∞,-2);
(2)证明:由(1)得:f(x)=x2+2x,即φ(x)=f(x)h(x)-$\frac{1}{x}$,(x>0),
设0<x1<x2,则x1-x2<0,x1x2>0,∴$\frac{{x}_{1}{-x}_{2}}{{{x}_{1}x}_{2}}$<0,
∵f(x)在(0,+∞)递增且f(x)>0,
∴f(x2)>f(x1)>0,
∵${e}^{{x}_{2}}$>${e}^{{x}_{1}}$>0,∴f(x1)${e}^{{x}_{1}}$<f(x2)${e}^{{x}_{2}}$,
∴φ(x1)-φ(x2)=f(x1)${e}^{{x}_{1}}$-f(x2)${e}^{{x}_{2}}$+$\frac{{x}_{1}{-x}_{2}}{{{x}_{1}x}_{2}}$<0,
即φ(x1)<φ(x2),∴φ(x)在(0,+∞)递增;
∵φ($\frac{1}{2}$)=$\frac{5}{4}$$\sqrt{c}$-2>$\frac{5}{4}$$\sqrt{2.56}$-2=0,
φ($\frac{1}{e}$)=$\frac{2e+1}{{e}^{2}}$${e}^{\frac{1}{e}}$-e<${e}^{\frac{1}{e}}$-e<0,
即φ($\frac{1}{2}$)φ($\frac{1}{e}$)<0,
∴函数y=f(x)h(x)-$\frac{1}{x}$(x>0)恰有1个零点x0,且x0∈($\frac{1}{e}$,$\frac{1}{2}$),
∴(${{x}_{0}}^{2}$+2x0)${e}^{{x}_{0}}$-$\frac{1}{{x}_{0}}$=0,即${e}^{{x}_{0}}$=$\frac{1}{{{(x}_{0}}^{2}+{2x}_{0}{)x}_{0}}$,
∴${{x}_{0}}^{2}$h(x0)-g(x0)=${{x}_{0}}^{2}$$\frac{1}{{{(x}_{0}}^{2}+{2x}_{0}{)x}_{0}}$-lnx0=$\frac{1}{{x}_{0}+2}$-lnx0,
∵y=$\frac{1}{x+2}$-lnx在(0,$\frac{1}{2}$)上是减函数,
∴$\frac{1}{{x}_{0}+2}$-lnx0>$\frac{2}{5}$-ln$\frac{1}{2}$=$\frac{2}{5}$+ln2>$\frac{2}{5}$+0.6=1,
即g(x0)<${{x}_{0}}^{2}$h(x0)-1,
综上,函数y=f(x)h(x)-$\frac{1}{x}$(x>0)恰有一个零点x0,且g(x0)<x02h(x0)-1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数的零点问题,是一道综合题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
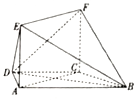 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
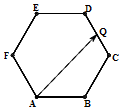
| A. | $\overrightarrow{AB}•\overrightarrow{AQ}$ | B. | $\overrightarrow{AC}•\overrightarrow{AQ}$ | C. | $\overrightarrow{AD}•\overrightarrow{AQ}$ | D. | $\overrightarrow{AE}•\overrightarrow{AQ}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com