
如图1,在等腰梯形CDEF中,CB、DA是梯形的高,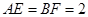 ,
,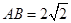 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使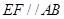 且
且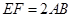 ,得一简单组合体
,得一简单组合体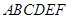 如图2示,已知
如图2示,已知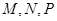 分别为
分别为 的中点.
的中点.


图1 图2
(1)求证: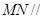 平面
平面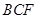 ;
;
(2)求证:
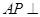
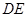 ;
;
(3)当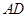 多长时,平面
多长时,平面 与平面
与平面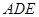 所成的锐二面角为
所成的锐二面角为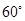 ?
?
(1)主要是得到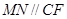 (2)关键是证明
(2)关键是证明 平面
平面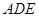 ,(3)
,(3)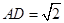
【解析】
试题分析:(1)证明:连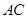 ,∵四边形
,∵四边形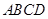 是矩形,
是矩形,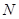 为
为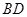 中点,
中点,
∴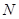 为
为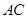 中点,
中点,
在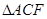 中,
中,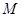 为
为 中点,则
中点,则 为
为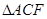 的中位线
的中位线
故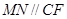
∵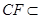 平面
平面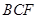 ,
,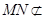 平面
平面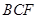 ,
, 平面
平面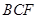 ;
;
(其它证法,请参照给分)

(2)依题意知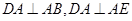 且
且
∴ 平面
平面
∵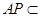 平面
平面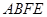 ,∴
,∴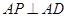 ,
,
∵ 为
为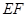 中点,∴
中点,∴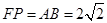
结合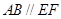 ,知四边形
,知四边形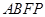 是平行四边形
是平行四边形
∴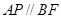 ,
,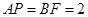
而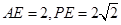 ,∴
,∴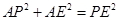 ∴
∴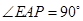 ,即
,即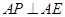 --8分
--8分
又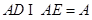 ∴
∴ 平面
平面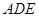 ,
,
∵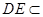 平面
平面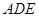 , ∴
, ∴
 .
.
(3)解:如图,分别以 所在的直线为
所在的直线为 轴建立空间直角坐标系
轴建立空间直角坐标系

设 ,则
,则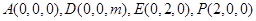
易知平面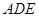 的一个法向量为
的一个法向量为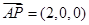 ,
,
设平面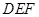 的一个法向量为
的一个法向量为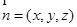 ,
,
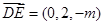 则
则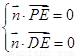 故
故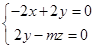 ,即
,即
令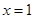 ,则
,则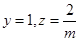 ,故
,故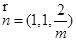
∴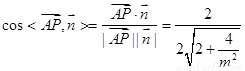 ,
,
依题意,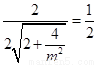 ,解得
,解得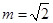 ,
,
即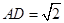 时,平面
时,平面 与平面
与平面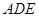 所成的锐二面角为
所成的锐二面角为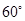 .
.
考点:直线与平面垂直的判定定理;直线与平面平行的判定定理;二面角
点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。在求二面角的平面角时,常利用向量来求解。


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
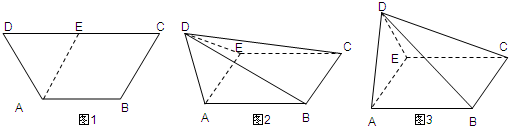 如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.
如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
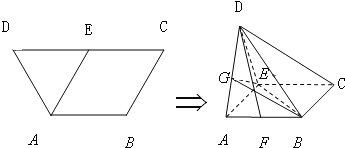 在如图1所示的等腰梯形ABCD中,AB∥CD,且AB=AD=BC=
在如图1所示的等腰梯形ABCD中,AB∥CD,且AB=AD=BC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012年山东省高考数学压轴卷(理科)(解析版) 题型:解答题
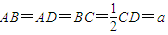 ,E为CD中点.若沿AE将三角形DAE折起,使平面DAE⊥平面ABCE,连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,使平面DAE⊥平面ABCE,连接DB,DC,得到如图2所示的几何体D-ABCE,在图2中解答以下问题:
查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷10(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com