练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设圆x2＋y2＝2的切线l与x轴正半轴、y轴正半轴分别交于点A，B，当|AB|取最小值时，切线l的方程为________．

     

    x＋y－2＝0

    【解析】设点A，B的坐标分别为A(a,0)，B(0，b)(a，b>0)，则直线AB的方程为＝1，即bx＋ay－ab＝0，因为直线AB和圆相切，所以圆心到直线AB的距离d＝＝，整理得＝ab，即2(a2＋b2)＝(ab)2≥4ab，所以ab≥4，当且仅当a＝b时取等号，又|AB|＝＝≥2，所以|AB|的最小值为2，此时a＝b，即a＝b＝2，切线l的方程为，即x＋y－2＝0.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练15练习卷（解析版） 题型：解答题

    设F1，F2分别是椭圆E：x2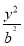＋＝1(0<b<1)的左、右焦点，过F1的直线l与E相交于A，B两点，且|AF2|，|AB|，|BF2|成等差数列．

    (1)求|AB|；

    (2)若直线l的斜率为1，求b的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练12练习卷（解析版） 题型：选择题

    已知两条直线a，b与两个平面α，β，b⊥α，则下列命题中正确的是(　　)．

    ①若a∥α，则a⊥b；②若a⊥b，则a∥α；③若b⊥β，则α∥β；④若α⊥β，则b∥β.

    A．①③ B．②④ C．①④ D．②③

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练10练习卷（解析版） 题型：填空题

    在正项数列{an}中，a1＝2，an＋1＝2an＋3×5n，则数列{an}的通项公式为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷5练习卷（解析版） 题型：解答题

    已知直线l：y＝x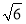＋，圆O：x2＋y2＝5，椭圆E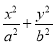：＝1(a>b>0)的离心率e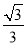＝，直线l被圆O截得的弦长与椭圆的短轴长相等．

    (1)求椭圆E的方程；

    (2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两条切线的斜率之积为定值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷5练习卷（解析版） 题型：选择题

    已知直线y＝k(x－m)与抛物线y2＝2px(p>0)交于A，B两点，且OA⊥OB，OD⊥AB于点D.若动点D的坐标满足方程x2＋y2－4x＝0，则m等于(　　)．

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷4练习卷（解析版） 题型：解答题

    如图，ABCD是块矩形硬纸板，其中AB＝2AD，AD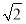＝，E为DC的中点，将它沿AE折成直二面角D-AE-B.

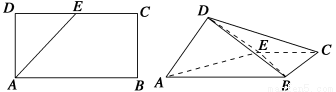
    (1)求证：AD⊥平面BDE；

    (2)求二面角B-AD-E的余弦值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷3练习卷（解析版） 题型：解答题

    已知数列{an}和{bn}满足：a1＝λ，an＋1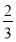＝an＋n－4，bn＝(－1)n(an－3n＋21)，其中λ为实数，n为正整数．

    (1)对任意实数λ，证明：数列{an}不是等比数列；

    (2)试判断数列{bn}是否为等比数列，并证明你的结论．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：解答题

    如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E.

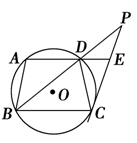
    (1)求证：AB2＝DE·BC；

    (2)若BD＝9，AB＝6，BC＝9，求切线PC的长．

     

    查看答案和解析>>

    同步练习册答案