|
|
|
若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0,则m=
|
| [ ] |
A. |
21
|
B. |
19
|
C. |
9
|
D. |
-11
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人教A版(新课标) 选修4-1 几何证明选讲
题型:
|
|
|
在△ABC中,sinA=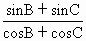 ,判断△ABC的形状并证明. ,判断△ABC的形状并证明.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为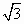 ,求二面角A1-AB-C的大小. ,求二面角A1-AB-C的大小.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若三角形 ABC的内角满足sinA+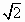 sinB=2sinC,则cosC的最小值是________. sinB=2sinC,则cosC的最小值是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设命题p: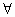 x∈R,x2+1>0,则 x∈R,x2+1>0,则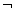 p为 p为
|
| [ ] |
A. |
 x0∈R,x x0∈R,x +1>0 +1>0
|
B. |
 x0∈R,x x0∈R,x +1≤0 +1≤0
|
C. |
 x0∈R,x x0∈R,x +1<0 +1<0
|
D. |
 x0∈R,x x0∈R,x +1≤0 +1≤0
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
复数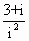 (i为虚数单位)的实部等于________. (i为虚数单位)的实部等于________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
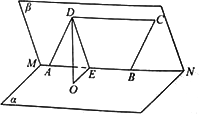
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若变量x,y满足约束条件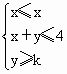 ,且z=2x+y的最小值为-6,则k=________. ,且z=2x+y的最小值为-6,则k=________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是
|
| [ ] |
A. |
(-∞,-2]
|
B. |
(-∞,-1]
|
C. |
[2,+∞)
|
D. |
[1,+∞)
|
|
|
查看答案和解析>>
