
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足下列条件的有两个的是( )
A.![]()
B.![]()
C.a=1,b=2,c=3
D.a=3,b=2,A=60°
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1 , F2 , 线段OF1 , OF2的中点分别为B1 , B2 , 且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2 , 求直线l的方程 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,Sn是其前n项和.已知a1+a3=16,S4=28.
(1)求数列{an}的通项公式
(2)当n取何值时Sn最大,并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,AC⊥BC,AC=BC= ![]() AA1=2,D是AC的中点.
AA1=2,D是AC的中点. 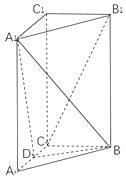
(1)求证:B1C∥平面A1BD;
(2)求直线AC与平面A1BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量对岸A,B两点的距离,沿河岸选取C,D两点,测得CD=2km,∠CDB=∠ADB=30°,∠ACD=60°,∠ACB=45°,求A,B两点的距离. 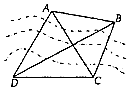
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,a2=2,b1=2,且对任意的正整数i,j,k,l,当i+j=k+l时,都有ai+bj=ak+bl , 则 ![]() 的值是( )
的值是( )
A.2012
B.2013
C.2014
D.2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时, ![]() ,函数
,函数 ![]() ,则关于x的不等式f(x)<g(x)的解集为( )
,则关于x的不等式f(x)<g(x)的解集为( )
A.(﹣2,﹣1)∪(﹣1,0)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com