分析:(1)以A为原点,
、
、
分别为x轴、y轴、z轴的正方向,AB的长度为单位长度建立空间直角坐标系,写出要用的点的坐标,构造向量,根据向量垂直得到线面垂直.
(2)根据所给的条件先证明线与面垂直,这样就做出这条垂线是要求的三棱锥的高,只要做出对应的底的面积就可以得到体积.
(3)建立坐标系,写出要用的点的坐标,构造向量,设出平面的法向量,求出法向量,根据两个向量所成的角的余弦,确定两个平面的夹角的余弦值,注意观察余弦值的符号.
解答: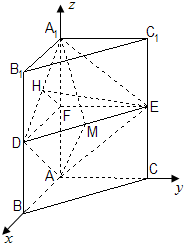
解:(1)以A为原点,
、
、
分别为x轴、y轴、z轴的正方向,AB的长度为单位长度建立空间直角坐标系.
由题设知点A,A
1,D,E,M的坐标分别为
(0,0,0),(0,0,2),(1,0,1),(0,1,1),(,,1).
∴
=(0,0,2),
=(-1,1,0),
=
(,,1)∴
•=0,•=0
∴AA
1⊥DE,DE⊥AM,AM∩AA
1=A,AM?平面AMA
1,AA
1?平面AMA
1
∴DE⊥平面AMA
1(2)取AA
1的中点F,连DF,EF
∴DF
=∥AB=1,EF
=∥AC=1∴DF⊥AA
1,DF⊥EF
又AA
1∩EF=F,AA
1?平面AA
1E,EF?平面AA
1E
∴DF⊥平面AA
1E∴
VA1-ADE=VD-A1AE=
•S△A1AE•DF=
××AA1×EF×DF=
×2×1×1=
(3)以A为原点,
、
、
分别为x轴、y轴、z轴的正方向,AB的长度为单位长度建立空间直角坐标系.
由题设知点A,A
1,D,C,E的坐标分别为(0,0,0),(0,0,2),(1,0,1),(0,1,0),(0,1,1).
∴
=(0,1,-1),
=(1,0,-1),
=(0,1,0)
设平面A
1DE的法向量为
=(x,y,z)?,取x=1,得
=(1,1,1).
∵AB⊥AC,AA
1⊥AC,
∴AC⊥平面A
1DA
cos?,>===.
结合图象知二面角A-DA
1-E的余弦值是
.
点评:本题考查空间向量求二面角,本题解题的关键是建立坐标系,把难度比较大的二面角的求法和线面之间的位置关系,转化成了数字的运算.此类题由于运算量大,易运算出错,解题时谨记.

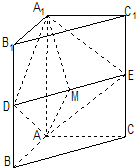 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=2,D、E分别是BB1、CC1的中点,M是DE的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=2,D、E分别是BB1、CC1的中点,M是DE的中点. 解:(1)以A为原点,
解:(1)以A为原点,

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案



