
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCDEFGH材料切割成三棱锥HACF.
(1)若点M,N,K分别是棱HA,HC,HF的中点,点G是NK上的任意一点,求证:MG∥平面ACF;
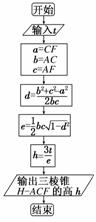
(2)已知原长方体材料中,AB=2 m,AD=3 m,DH=1 m,根据艺术品加工需要,工程师必须求出该三棱锥的高.工程师设计了一个求三棱锥的高度的程序,其框图如图所示,则运行该程序时乙工程师应输入的t的值是多少?
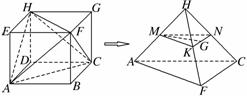
(1)证明:∵HM=MA,HN=NC,HK=KF,∴MK∥AF,MN∥AC.
∵MK⊄平面ACF,AF⊂平面ACF,∴MK∥平面ACF,
同理可证MN∥平面ACF,
∵MN,MK⊂平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,又MG⊂平面MNK,故MG∥平面ACF.
(2)由程序框图可知a=CF,b=AC,c=AF,
∴d=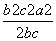 =
=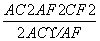 =cos∠CAF,
=cos∠CAF,
∴e=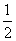 bc
bc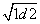 =
=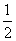 AC·AF·sin∠CAF=S△ACF.
AC·AF·sin∠CAF=S△ACF.
又h=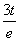 ,∴t=
,∴t=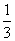 he=
he=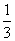 h·S△ACF=V三棱锥HACF.
h·S△ACF=V三棱锥HACF.
∵三棱锥HACF为将长方体ABCDEFGH切掉4个体积相等的小三棱锥所得,
∴V三棱锥HACF=2×3×1-4×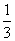 ×
×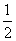 ×3×2×1=6-4=2,故t=2.
×3×2×1=6-4=2,故t=2.


科目:高中数学 来源: 题型:
已知函数,f(x)=Asin(cox+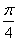 )(其中x∈R,A>0,
)(其中x∈R,A>0,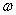 >0)的最大值为2,最小正周期为8.
>0)的最大值为2,最小正周期为8.
(I)求函数f(x)的解析式及单调递增区间:
(II)若函数f(x)图象上的两点P,Q的横坐标依次为2.4,O为坐标原点,求△POQ的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
对某同学的6次物理测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法:①中位数为84; ②众数为85;③平均数为85; ④极差为12.
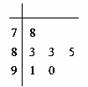
其中,正确说法的序号是( )
A. ①② B.③④ C. ②④ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:“∀x∈[1,2],x2- ≥0”,命题q:“∃x∈R,x2+2
≥0”,命题q:“∃x∈R,x2+2 x+2-
x+2- =0”.若命题“
=0”.若命题“ p且q”是真命题,则实数
p且q”是真命题,则实数 的取值范围为________.
的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com