
| AB |
| AC |
| CP |
| ||
|
|
| ||
|
| 1 |
| x |
| 1 |
| y |
A.
| B.
| C.
| D.
|
| AB |
| AC |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
| CP |
| CA |
| CB |
| ||
|
|
| e1 |
| ||
|
|
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| CP |
| ||
|
|
| ||
|
|
| 1 |
| x |
| 1 |
| y |
| 1 |
| 12 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| 12 |
| 3y |
| x |
| 4x |
| y |
| 7 |
| 12 |
| ||
| 3 |
| 7 |
| 12 |
| ||
| 3 |
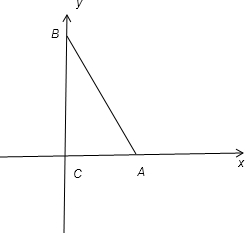


科目:高中数学 来源:不详 题型:解答题
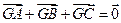 , ②
, ②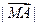 =
= 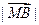 =
= 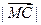 ③
③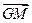 ∥
∥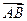
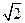 , 0) ,已知
, 0) ,已知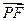 ∥
∥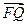 ,
, 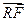 ∥
∥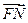 且
且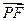 ·
·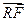 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
,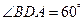 ,
, ,求两景点
,求两景点 与
与 的距离(精确到0.1km).参考数据:
的距离(精确到0.1km).参考数据:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 10 |
| MC |
| MD |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
| A.5 | B.7 | C.12 | D.13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com