练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知2<x<4，则的取值范围是_________________

    [5，6)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年南昌市一模理）（12分）已知函数f (x) =lnx,g(x) =，（a为常数），若直线l与y =f(x), y =g(x)的图象都相切，且l与y = f(x)的图象相切的切点的横坐标为1.

    （1）求直线l的方程及a的值；

    （2） 当 2 ≤m <时,求h(x)= f(x)―f(x)[2g(x)- m +1]在[,2]上的最大值.

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江省高二下学期期中考试文科数学试卷（解析版） 题型：解答题

    已知函数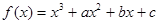在x=与x =l时都取得极值

    （1）求a、b的值与函数f（x）的单调区间

    （2）若对x∈（-1，2），不等式f（x）<c2恒成立，求c的取值范围。

     

    查看答案和解析>>

    科目：高中数学 来源：2013年黑龙江省高三第四次联考理科数学试卷（解析版） 题型：选择题

    已知集合A={x|－l≤x≤3}，集合B=|x|log2x<2}，则A B=

    A．{x|1≤x≤3}                           B．{x|－1≤x≤3}

    C．{x| 0<x≤3}                            D．{x|－1≤x<0}

     

    查看答案和解析>>

    科目：高中数学 来源：河北省期中题 题型：解答题

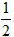    已知函数f(x)=㏑x-ax2+bx(a>0)且导数f‵(x)=0.
    （1）试用含有a的式子表示b，并求f(x)的单调区间；
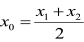    （2）对于函数图象上不同的两点A(x1,y1)，且x1<x2，如果在函数图像上存在点M(x0,y0)（其中x0∈(x1,x2)）使得点M处的切线l//AB，则称AB存在“相依切线”.特别地，当时，又称AB存在“中值相依切线”.试问：在函数f(x)上是否存在两点A,B使得它存在“中值相依切线”？若存在，求A,B的坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的导数f′(x)＝3x2－3ax，f(0)＝b，a，b为实数，1<a<2.

    (1)若f(x)在区间[－1,1]上的最小值、最大值分别为－2、1，求a、b的值；

    (2)在(1)的条件下，求经过点P(2,1)且与曲线f(x)相切的直线l的方程；

    (3)设函数F(x)＝[f′(x)＋6x＋1]·e2x，试判断函数F(x)的极值点个数.

    查看答案和解析>>

    同步练习册答案